��Ŀ����
����С������12�֣���ֱ������ƽ������һ����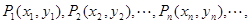 ��һ��������n����Pn�ں���
��һ��������n����Pn�ں���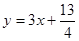 ��ͼ���ϣ���Pn�ĺ����깹����
��ͼ���ϣ���Pn�ĺ����깹����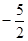 Ϊ�����1Ϊ����ĵȲ�����{xn}.
Ϊ�����1Ϊ����ĵȲ�����{xn}.
��1�����Pn�����ꣻ
��2������������C1��C2��C3������Cn�����е�ÿһ���ĶԳ��ᶼ��ֱ��x�ᣬ������Cn�Ķ���ΪPn���ҹ���Dn��0�� ��.����������Cn�����ڵ�Dn��ֱ�ߵ�б��Ϊkn����
��.����������Cn�����ڵ�Dn��ֱ�ߵ�б��Ϊkn����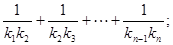
��3����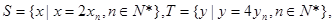 �Ȳ�����
�Ȳ�����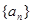 ����һ��
����һ��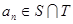 ������
������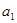 ��
��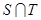 ��������
��������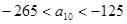 ��������
��������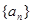 ��ͨ�ʽ.
��ͨ�ʽ.
���𰸡�
��1��
��2�� =
=
��3��
����������1�� ��
��

��2�� �ĶԳ��ᴹֱ��x�ᣬ�Ҷ���ΪPn������
�ĶԳ��ᴹֱ��x�ᣬ�Ҷ���ΪPn������ �ķ���Ϊ
�ķ���Ϊ
�� ����
���� �ķ���Ϊ
�ķ���Ϊ
�� ��
��
��

=
��3�� ��
��

 ����S
����S �������a1=��17.
�������a1=��17.
�� ����Ϊd����a10=
����Ϊd����a10= �ɴ˵�
�ɴ˵� �֡�
�֡�
�� ��
�� ����
����

��ϰ��ϵ�д�
�����Ŀ