ЬтФПФкШн
дкжБНЧзјБъЦНУцЩЯгавЛЕуСаP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЌЁЃЌЖдвЛЧае§ећЪ§nЃЌЕуPnдкКЏЪ§y=3x+| 13 |
| 4 |
| 5 |
| 2 |
ЃЈ1ЃЉЧѓЕуPnЕФзјБъЃЛ
ЃЈ2ЃЉЩшХзЮяЯпСаC1ЃЌC2ЃЌC3ЃЌЁЃЌCnЃЌЁжаЕФУПвЛЬѕЕФЖдГЦжсЖМДЙжБгкxжсЃЌХзЮяЯпCnЕФЖЅЕуЮЊPnЃЌЧвЙ§ЕуDnЃЈ0ЃЌn2+1ЃЉЃЎМЧгыХзЮяЯпCnЯрЧагкЕуDnЕФжБЯпЕФаБТЪЮЊknЃЌЧѓ
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
ЃЈ3ЃЉЩшS={x|x=2xnЃЌnЁЪN*}ЃЌT={y|y=4ynЃЌnЁЪN*}ЃЌЕШВюЪ§Са{an}ЕФШЮвЛЯюanЁЪSЁЩTЃЌЦфжаa1ЪЧSЁЩTжаЕФзюДѓЪ§ЃЌ-265ЃМa10ЃМ-125ЃЌЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЎ
ЗжЮіЃКЃЈ1ЃЉИљОнЕШВюЪ§СаЕФЭЈЯюЙЋЪНПЩЧѓЕУxnЃЌНјЖјДњШыжБЯпЗНГЬЧѓЕУynЃЌдђЕуPЕФзјБъПЩЕУЃЎ
ЃЈ2ЃЉЯШЩшГіCnЕФЗНГЬЃЌАбDЕуДњШыЧѓЕУaЃЌНјЖјЖдКЏЪ§НјааЧѓЕУЧѓЕУЧаЯпЕФаБТЪЃЌМДknЕФБэДяЪНЃЌНјЖјгУСбЯюЗЈЧѓЕУ
+
+Ё+
ЃЈ3ЃЉИљОнСНМЏКЯЕФЬиЕуПЩжЊSЁЩT=TЃЌНјЖјЭЦЖЯГіTжазюДѓЪ§a1=-17ЃЎЩш{an}ЙЋВюЮЊdЃЌдђИљОнa10ЕФЗЖЮЇЧѓЕУdЕФЗЖЮЇЃЌНјЖјИљОнd=-12mЧѓЕУdЕФжЕЃЎдђЪ§Са{an}ЕФЭЈЯюЙЋЪНПЩЕУЃЎ
ЃЈ2ЃЉЯШЩшГіCnЕФЗНГЬЃЌАбDЕуДњШыЧѓЕУaЃЌНјЖјЖдКЏЪ§НјааЧѓЕУЧѓЕУЧаЯпЕФаБТЪЃЌМДknЕФБэДяЪНЃЌНјЖјгУСбЯюЗЈЧѓЕУ
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
ЃЈ3ЃЉИљОнСНМЏКЯЕФЬиЕуПЩжЊSЁЩT=TЃЌНјЖјЭЦЖЯГіTжазюДѓЪ§a1=-17ЃЎЩш{an}ЙЋВюЮЊdЃЌдђИљОнa10ЕФЗЖЮЇЧѓЕУdЕФЗЖЮЇЃЌНјЖјИљОнd=-12mЧѓЕУdЕФжЕЃЎдђЪ§Са{an}ЕФЭЈЯюЙЋЪНПЩЕУЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉЁпxn=-
+(n-1)ЁС(-1)=-n-
ЃЌ
Ёрyn=3xn+
=-3n-
ЃЎ
ЁрPn(-n-
ЃЌ-3n-
)ЃЎ
ЃЈ2ЃЉЁпCnЕФЖдГЦжсДЙжБгкxжсЃЌЧвЖЅЕуЮЊPnЃЌ
ЁрЩшCnЕФЗНГЬЮЊy=a(x+
)2-
ЃЎ
АбDnЃЈ0ЃЌn2+1ЃЉДњШыЩЯЪНЃЌЕУa=1ЃЌ
ЁрCnЕФЗНГЬЮЊy=x2+ЃЈ2n+3ЃЉx+n2+1ЃЎ
Ёпkn=y'|x=0=2n+3ЃЌ
Ёр
=
=
[
-
]ЃЌ
Ёр
+
+
=
[(
-
)+(
-
)++(
-
)]
=
(
-
)=
-
ЃЎ
ЃЈ3ЃЉT={y|y=-ЃЈ12n+5ЃЉЃЌnЁЪN*}={y|y=-2ЃЈ6n+1ЃЉ-3ЃЌnЁЪN*}ЃЌ
ЁрSЁЩT=TЃЌTжазюДѓЪ§a1=-17ЃЎ
Щш{an}ЙЋВюЮЊdЃЌдђa10=-17+9dЁЪЃЈ-265ЃЌ-125ЃЎЃЉгЩДЫЕУ-
ЃМdЃМ-12ЃЎ
гжЁпanЁЪTЃЎ
Ёрd=-12mЃЈmЁЪN*ЃЉ
Ёрd=-24ЃЌ
Ёрan=7-24nЃЈnЁЪN*ЃЌnЁн2ЃЉЃЎ
| 5 |
| 2 |
| 3 |
| 2 |
Ёрyn=3xn+
| 13 |
| 4 |
| 5 |
| 4 |
ЁрPn(-n-
| 3 |
| 2 |
| 5 |
| 4 |
ЃЈ2ЃЉЁпCnЕФЖдГЦжсДЙжБгкxжсЃЌЧвЖЅЕуЮЊPnЃЌ
ЁрЩшCnЕФЗНГЬЮЊy=a(x+
| 2n+3 |
| 2 |
| 12n+5 |
| 4 |
АбDnЃЈ0ЃЌn2+1ЃЉДњШыЩЯЪНЃЌЕУa=1ЃЌ
ЁрCnЕФЗНГЬЮЊy=x2+ЃЈ2n+3ЃЉx+n2+1ЃЎ
Ёпkn=y'|x=0=2n+3ЃЌ
Ёр
| 1 |
| kn-1kn |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| (2n+1) |
| 1 |
| (2n+3) |
Ёр
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
=
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2n+3 |
| 1 |
| 10 |
| 1 |
| 4n+6 |
ЃЈ3ЃЉT={y|y=-ЃЈ12n+5ЃЉЃЌnЁЪN*}={y|y=-2ЃЈ6n+1ЃЉ-3ЃЌnЁЪN*}ЃЌ
ЁрSЁЩT=TЃЌTжазюДѓЪ§a1=-17ЃЎ
Щш{an}ЙЋВюЮЊdЃЌдђa10=-17+9dЁЪЃЈ-265ЃЌ-125ЃЎЃЉгЩДЫЕУ-
| 248 |
| 9 |
гжЁпanЁЪTЃЎ
Ёрd=-12mЃЈmЁЪN*ЃЉ
Ёрd=-24ЃЌ
Ёрan=7-24nЃЈnЁЪN*ЃЌnЁн2ЃЉЃЎ
ЕуЦРЃКБОЬтжївЊПМВщСЫЪ§СаЧѓКЭЮЪЬтЃЎПМВщСЫгУСбЯюЗЈЧѓКЭЕФЗНЗЈдЫгУКЭЖдЪ§СаЛљДЁжЊЪЖЕФзлКЯдЫгУЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
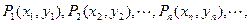 ЖдвЛЧае§ећЪ§nЃЌЕуPnдкКЏЪ§
ЖдвЛЧае§ећЪ§nЃЌЕуPnдкКЏЪ§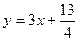 ЕФЭМЯѓЩЯЃЌЧвPnЕФКсзјБъЙЙГЩвд
ЕФЭМЯѓЩЯЃЌЧвPnЕФКсзјБъЙЙГЩвд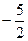 ЮЊЪзЯюЃЌЃ1ЮЊЙЋВюЕФЕШ
ЮЊЪзЯюЃЌЃ1ЮЊЙЋВюЕФЕШ ВюЪ§Са{xn}.
ВюЪ§Са{xn}.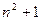 ЃЉ.МЧгыХзЮяЯпCnЯрЧагкЕуDnЕФжБЯпЕФаБТЪЮЊknЃЌЧѓ
ЃЉ.МЧгыХзЮяЯпCnЯрЧагкЕуDnЕФжБЯпЕФаБТЪЮЊknЃЌЧѓ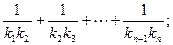
 Щш
Щш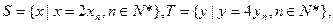 ЕШВюЪ§Са
ЕШВюЪ§Са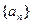 ЕФШЮвЛЯю
ЕФШЮвЛЯю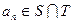 ЃЌЦфжа
ЃЌЦфжа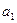 ЪЧ
ЪЧ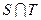 жаЕФзюДѓЪ§ЃЌ
жаЕФзюДѓЪ§ЃЌ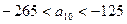 ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са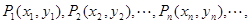 ЖдвЛЧае§ећЪ§nЃЌЕуPnдкКЏЪ§
ЖдвЛЧае§ећЪ§nЃЌЕуPnдкКЏЪ§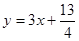 ЕФЭМЯѓЩЯЃЌЧвPnЕФКсзјБъЙЙГЩвд
ЕФЭМЯѓЩЯЃЌЧвPnЕФКсзјБъЙЙГЩвд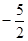 ЮЊЪзЯюЃЌЃ1ЮЊЙЋВюЕФЕШВюЪ§Са{xn}.
ЮЊЪзЯюЃЌЃ1ЮЊЙЋВюЕФЕШВюЪ§Са{xn}. ЃЉ.МЧгыХзЮяЯпCnЯрЧагкЕуDnЕФжБЯпЕФаБТЪЮЊknЃЌЧѓ
ЃЉ.МЧгыХзЮяЯпCnЯрЧагкЕуDnЕФжБЯпЕФаБТЪЮЊknЃЌЧѓ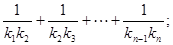
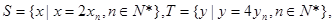 ЕШВюЪ§Са
ЕШВюЪ§Са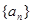 ЕФШЮвЛЯю
ЕФШЮвЛЯю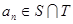 ЃЌЦфжа
ЃЌЦфжа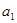 ЪЧ
ЪЧ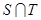 жаЕФзюДѓЪ§ЃЌ
жаЕФзюДѓЪ§ЃЌ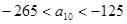 ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са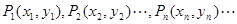 ЃЌЖдвЛЧае§ећЪ§
ЃЌЖдвЛЧае§ећЪ§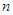 ЃЌЕу
ЃЌЕу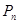 ЮЛгкКЏЪ§
ЮЛгкКЏЪ§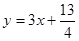 ЕФЭМЯѓЩЯЃЌЧв
ЕФЭМЯѓЩЯЃЌЧв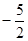 ЮЊЪзЯюЃЌ
ЮЊЪзЯюЃЌ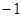 ЮЊЙЋВюЕФЕШВюЪ§Са
ЮЊЙЋВюЕФЕШВюЪ§Са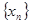 ЁЃ
ЁЃ жаЕФУПвЛЬѕЕФЖдГЦжсЖМДЙжБгк
жаЕФУПвЛЬѕЕФЖдГЦжсЖМДЙжБгк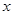 жсЃЌЕк
жсЃЌЕк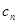 ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ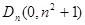 ЃЌМЧгыЪ§Са
ЃЌМЧгыЪ§Са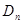 ЕФжБЯпЕФаБТЪЮЊ
ЕФжБЯпЕФаБТЪЮЊ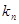 ЃЌЧѓЃК
ЃЌЧѓЃК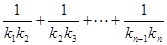 ЁЃ
ЁЃ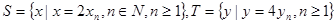 ЃЌЕШВюЪ§Са
ЃЌЕШВюЪ§Са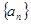 ЕФШЮвЛЯю
ЕФШЮвЛЯю ЃЌЦфжа
ЃЌЦфжа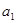 ЪЧ
ЪЧ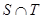 жаЕФзюДѓЪ§ЃЌ
жаЕФзюДѓЪ§ЃЌ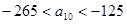 ЃЌЧѓ
ЃЌЧѓ