题目内容
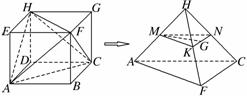
某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCDEFGH材料切割成三棱锥HACF.
(1)若点M,N,K分别是棱HA,HC,HF的中点,点G是NK上的任意一点,求证:MG∥平面ACF;
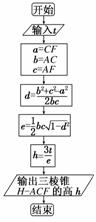
(2)已知原长方体材料中,AB=2 m,AD=3 m,DH=1 m,根据艺术品加工需要,工程师必须求出该三棱锥的高.工程师设计了一个求三棱锥的高度的程序,其框图如图所示,则运行该程序时乙工程师应输入的t的值是多少?
(1)证明:∵HM=MA,HN=NC,HK=KF,∴MK∥AF,MN∥AC.
∵MK⊄平面ACF,AF⊂平面ACF,∴MK∥平面ACF,
同理可证MN∥平面ACF,
∵MN,MK⊂平面MNK,且MK∩MN=M,
∴平面MNK∥平面ACF,又MG⊂平面MNK,故MG∥平面ACF.
(2)由程序框图可知a=CF,b=AC,c=AF,
∴d=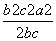 =
=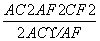 =cos∠CAF,
=cos∠CAF,
∴e=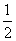 bc
bc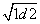 =
=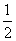 AC·AF·sin∠CAF=S△ACF.
AC·AF·sin∠CAF=S△ACF.
又h=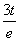 ,∴t=
,∴t=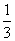 he=
he=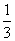 h·S△ACF=V三棱锥HACF.
h·S△ACF=V三棱锥HACF.
∵三棱锥HACF为将长方体ABCDEFGH切掉4个体积相等的小三棱锥所得,
∴V三棱锥HACF=2×3×1-4×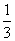 ×
×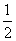 ×3×2×1=6-4=2,故t=2.
×3×2×1=6-4=2,故t=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
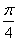 )(其中x∈R,A>0,
)(其中x∈R,A>0, >0)的最大值为2,最小正周期为8.
>0)的最大值为2,最小正周期为8.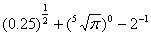 =______.
=______.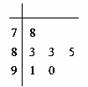
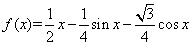 的图象在点
的图象在点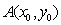 处的切线斜率为1,则
处的切线斜率为1,则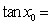 ________________.
________________. ,
, ,则
,则 = ( )
= ( ) ,则
,则 ( )
( ) B.
B. C
C D.
D.
 ≥0”,命题q:“∃x∈R,x2+2
≥0”,命题q:“∃x∈R,x2+2 p且q”是真命题,则实数
p且q”是真命题,则实数 ,则
,则 等于( )
等于( ) D.-4
D.-4