题目内容
已知三棱锥O ABC,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O
ABC,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O ABC的体积为
ABC的体积为 ,则球O的表面积是( )
,则球O的表面积是( )
(A)64π (B)16π (C) π (D)544π
π (D)544π
A解析:△ABC的面积是 ,由余弦定理得AC=
,由余弦定理得AC=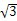 .
.
设球心O到平面ABC的距离为h,
则 ×
× ×h=
×h= ,
,
所以h= .
.
△ABC外接圆的直径2r= =2,
=2,
所以r=1.
球的半径R= =4,
=4,
故所求的球O的表面积是4π×42=64π.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
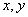 满足约束条件
满足约束条件 ,则
,则 的最大值是( )
的最大值是( ) -2(x<0),则f(x)有 ( )
-2(x<0),则f(x)有 ( )


 A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶
A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶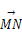 =α
=α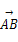 +β
+β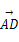 +γ
+γ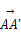 ,试求α,β,γ之值.
,试求α,β,γ之值.