题目内容
若两圆x2+y2-2x+10y+1=0，x2+y2-2x+2y-m=0相交，则m的取值范围为 ．
考点：圆与圆的位置关系及其判定
专题：直线与圆
分析：先求得两圆的圆心距d=4，再由圆心距大于半径之差而小于半径之和，求得m的取值范围．
解答：
解：圆x2+y2-2x+10y+1=0，即（x-1）2 +（y+5）2 =25，圆 x2+y2-2x+2y-m=0即 （x-1）2+（y+1）2=2+m，
故两圆的圆心距d=
=4，再由圆心距大于半径之差而小于半径之和，可得|5-
|＜4＜5+
，
∴
，或
，求得23≤m＜79，或-1＜m＜23．
综上可得，-1＜m＜79，
故答案为：（-1，79）．
故两圆的圆心距d=
| (1-1)2+(-5+1)2 |
| m+2 |
| m+2 |
∴
|
|
综上可得，-1＜m＜79，
故答案为：（-1，79）．
点评：本题主要考查圆和圆的位置关系的判断方法，两点间的距离公式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在长方体ABCDA1B1C1D1中，E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点．求证：平面A1EFD1∥平面BCF1E1．已知m，n是两条不同直线，α，β是两个不同的平面，且n?β，则下列叙述正确的是（ ）
| A、若m∥n，m?α，则α∥β |
| B、若α∥β，m?α，则m∥n |
| C、若m∥n，m⊥α，则α⊥β |
| D、若α∥β，m⊥n，则m⊥α |
设f（x）=
，若f2（x）-4f（x）+m=0有四个不同的实根，则实数m的可取值范围是（ ）
|
| A、[3，4] |
| B、（3，4] |
| C、（3，4） |
| D、[3，4） |
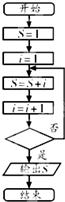阅读如图所示的程序框图（ 框图中的赋值符号“=”也可以写成“←”或“：=”），若输出S的值等于7，那么在程序框图中的判断框内应填写的条件是（ ）| A、i＞2？ | B、i＞3？ |
| C、i＞4？ | D、i＞5？ |