题目内容
14.已知函数f(x)定义在R上的偶函数,且在[0,+∞)上为减函数,若f(log2m)+f(log${\;}_{\frac{1}{2}}$m)≤2f(1),则m的取值范围是( )| A. | [2,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,2] | D. | (0,$\frac{1}{2}$]∪[2,+∞) |
分析 由偶函数的性质将f(log2m)+f(log${\;}_{\frac{1}{2}}$m)≤2f(1),化为:f(log2m)≤f(1),再由f(x)的单调性列出不等式,根据对数函数的性质求出m的取值范围.
解答 解:因为函数f(x)是定义在R上的偶函数,
所以f(log${\;}_{\frac{1}{2}}$m)=f(log2m)f(log2m),
则f(log2m)+f(log${\;}_{\frac{1}{2}}$m)≤2f(1)为:f(log2m)≤f(1),
因为函数f(x)在区间[0,+∞)上为减函数
所以|log2m|≥1,解得0<m≤$\frac{1}{2}$或m≥2,
则m的取值范围是(0,$\frac{1}{2}$]∪[2,+∞).
故选:D
点评 本题考查函数的奇偶性、单调性的应用,以及对数函数的性质,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
6.已知数列{an},它的前n项和为Sn,若an=$\frac{1}{(2n+1)(2n-1)}$,则Sn=( )
| A. | $\frac{2}{2n+1}$ | B. | $\frac{2n}{2n+1}$ | C. | $\frac{n}{2n+1}$ | D. | $\frac{1}{2n+1}$ |
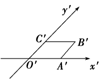 在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.
在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.