题目内容
14.已知复数z=lgm+(lgn)i,其中i是虚数单位.若复数z在复平面内对应的点在直线y=-x上,则mn的值等于( )| A. | 0 | B. | 1 | C. | 10 | D. | $\frac{1}{10}$ |
分析 复数z=lgm+(lgn)i,复数z在复平面内对应的点(lgm,lgn)在直线y=-x上,可得lgm=-lgn,化简即可得出.
解答 解:复数z=lgm+(lgn)i,复数z在复平面内对应的点(lgm,lgn)在直线y=-x上,
∴lgm=-lgn,可得lg(mn)=0,可得mn=1.
故选:B.
点评 本题考查了复数的几何意义、对数运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
2.定义在R上的函数f(x)的图象关于直线x=2对称,且f(x)满足:对任意的x1,x2∈(-∞,2](x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$,且f(4)=0,则关于x不等式$\frac{f(x)}{x}<0$的解集是( )
| A. | (-∞,0)∪(4,+∞) | B. | (0,2)∪(4,+∞) | C. | (-∞,0)∪(0,4) | D. | (0,2)∪(2,4) |
3.设A(-5,0),B(5,0),M为平面上的动点,若当|MA|-|MB|=10时,M的轨迹为( )
| A. | 双曲线的一支 | B. | 一条线段 | C. | 一条射线 | D. | 两条射线 |
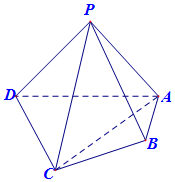 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.