题目内容
选修4-4:坐标系与参数方程
已知直线l的参数方程为
(t为参数),曲线C的参数方程为
(θ为参数),设直线l与曲线C交于A、B两点.
(1)求直线l与曲线C的普通方程;
(2)设P(2,0),求|PA|•|PB|的值.
已知直线l的参数方程为
|
|
(1)求直线l与曲线C的普通方程;
(2)设P(2,0),求|PA|•|PB|的值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:分别消去参数得到直线和曲线的普通方程;将直线方程与曲线方程联立方程组,利用根与系数的关系得到解答.
解答:
解:(1)直线l的方程为x-y-2=0,曲线C:
+
=1;
(2)将直线l的方程与曲线C联立方程组得
,消去y得7x2-36x-32=0,
所以x1+x2=
,x1x2=-
,
P(2,0),|PA|•|PB|=
|x1-2|+
|x2-2|=
|x1-x2|=
=
=
.
| x2 |
| 16 |
| y2 |
| 12 |
(2)将直线l的方程与曲线C联立方程组得
|
所以x1+x2=
| 16 |
| 7 |
| 32 |
| 7 |
P(2,0),|PA|•|PB|=
| 2 |
| 2 |
| 2 |
| 2 |
| (x1+x2)2-4x 1x2 |
| 2 |
|
| 48 |
| 7 |
点评:本题考查了参数方程化为普通方程的方法,以及利用根与系数的关系解决弦长问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
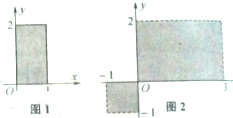 如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合:
如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合: