题目内容
若圆x2+y2=2在点(1,1)处的切线与双曲线
-
=1的一条渐近线垂直,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
考点:双曲线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:首先求出圆的切线方程,进一步求出双曲线的离心率.
解答:
解:圆x2+y2=2在点(1,1)处的切线的斜率与切点与圆心的连线垂直,
所以切线的斜率为:k=-1
设切线的方程为:y=-x+b
利用圆心到直线的距离等于半径解得b=
则切线方程为:y=-x+
由于:y=-x+
与双曲线的渐近线垂直则:
=1
进一步利用c2=a2+b2
解得:e=
=
故选:A
所以切线的斜率为:k=-1
设切线的方程为:y=-x+b
利用圆心到直线的距离等于半径解得b=
| 2 |
则切线方程为:y=-x+
| 2 |
由于:y=-x+
| 2 |
| b |
| a |
进一步利用c2=a2+b2
解得:e=
| c |
| a |
| 2 |
故选:A
点评:本题考查的知识要点:点到直线的距离,圆的切线方程,双曲线的离心率,及双曲线中a、b、c的关系式.

练习册系列答案
相关题目
在△ABC中,已知角A,B,C所对的边分别为a,b,c,且a=3,c=8,B=60°,则△ABC的周长是( )
| A、17 | B、19 | C、16 | D、18 |
数列{an}的通项公式an=n2+2n,则数列{
}的前10项和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图是2014年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,该数据的中位数和众数依次为( )
如图是2014年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,该数据的中位数和众数依次为( )| A、86,84 |
| B、84,84 |
| C、84,86 |
| D、85,86 |
 已知函数f(x)=x-
已知函数f(x)=x-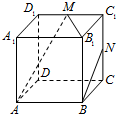 如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论:
如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论: