题目内容
2.已知变量x,y满足$\left\{\begin{array}{l}x-3y+3≤0\\ x≥1\\ x+y-4≤0\end{array}\right.$则$\frac{x}{y}$的最大值是( )| A. | $\frac{9}{7}$ | B. | 3 | C. | $\frac{3}{4}$ | D. | $\frac{7}{9}$ |
分析 画出约束条件的可行域,利用目标函数的几何意义,转化求解即可.
解答 解:令$k=\frac{y}{x}$,则k表示可行域内的点与原点连线的斜率,变量x,y满足$\left\{\begin{array}{l}x-3y+3≤0\\ x≥1\\ x+y-4≤0\end{array}\right.$的可行域如图: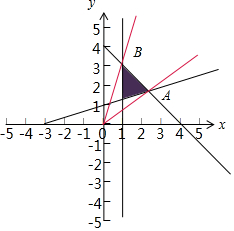
由图形可知kOA≤k≤kOB,联立方程$\left\{\begin{array}{l}{x-3y+3=0}\\{x+y-4=0}\end{array}\right.$与$\left\{\begin{array}{l}{x=1}\\{x+y-4=0}\end{array}\right.$可以求出$A({\frac{9}{4},\frac{7}{4}}),B({1,3})$,
所以$\frac{7}{9}≤k≤3$,
故$\frac{1}{k}$的最大值为$\frac{9}{7}$.
故选:A.
点评 本题考查线性规划,判断目标函数的几何意义是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
12.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则MN和CD1所成角的大小为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
14.已知偶函数f(x)在区间(-∞,0]内单调递减,a=f(log23),b=f(log45),$c=f({2^{\frac{1}{2}}})$,则a,b,c满足( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
11.直线x=a分别与曲线y=2(x+1),y=x+lnx交于A、B两点,则|AB|的最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3}{2}$ |
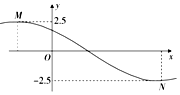 已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )
已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )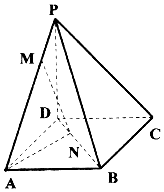 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.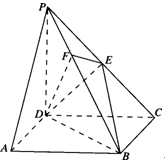 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.