题目内容
5．设等差数列{an}的前n项和为Sn，且a1＞0，a2+a9＞0，a5a6＜0，则满足Sn＞0的最大自然数n的值为（ ）| A． | 5 | B． | 6 | C． | 10 | D． | 11 |
分析 a2+a9=a5+a6＞0，a5a6＜0，可得a5＞0，a6＜0，再利用等差数列的通项公式及其性质与求和公式即可得出．
解答 解：∵a2+a9=a5+a6＞0，a5a6＜0，
∴a5＞0，a6＜0，$由{a_5}=\frac{{{a_1}+{a_9}}}{2}得{S_9}=\frac{{9（{a_1}+{a_9}）}}{2}＞0$，
由a6=$\frac{{a}_{1}+{a}_{11}}{2}$，可得S11=$\frac{11（{a}_{1}+{a}_{11}）}{2}$=11a6＜0．
S10=$\frac{10（{a}_{1}+{a}_{10}）}{2}$=5（a2+a9）＞0，
综上可知满足Sn＞0的最大自然数n的值为10．
故选：C．
点评 本题考查了等差数列的通项公式及其性质与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
19．已知b-2n=π3m（b＞0，m，n∈N+），则b=（ ）
| A． | π${\;}^{\frac{3m}{2n}}$（m，n∈N+） | B． | π${\;}^{-\frac{3m}{2n}}$（m，n∈N+） | C． | π${\;}^{\frac{2n}{3m}}$（m，n∈N+） | D． | π${\;}^{-\frac{2n}{3m}}$（m，n∈N+） |
16．函数y=sin（2x+φ），φ∈（0，2π）的部分图象如图所示，则φ的值为（ ）
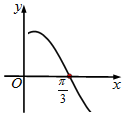
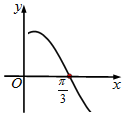
| A． | $\frac{π}{3}$ | B． | $\frac{4π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{π}{3}$或$\frac{4π}{3}$ |
14．已知复数z满足（1+3i）z=10，则z=（ ）
| A． | -1-3i | B． | 1+3i | C． | -1+3i | D． | 1-3i |