题目内容
3.下列各选项中叙述错误的是( )| A. | 命题“若x≠0,则x2-3x≠0”的否命题是“若x=0,则x2-3x=0” | |
| B. | 命题“?x∈R,lg(x2-x+1)≥0”是假命题 | |
| C. | 命题“?x∈R,3sinx=$\sqrt{3}$”是真命题 | |
| D. | 命题“若x=1,则向量$\overrightarrow{a}$=(-2x,1)与$\overrightarrow{b}$=(-2,x)共线”的逆命题是真命题 |
分析 A,根据命题的否命题,既要否定条件,又要否定结论的原则判定;
B,存在实数使x2-x+1<1;
C,由3sinx=$\sqrt{3}$得sinx∈[-1,1]得命题“?x∈R,3sinx=$\sqrt{3}$”是真命题;
D,若向量$\overrightarrow{a}$=(-2x,1)与$\overrightarrow{b}$=(-2,x)共线⇒-2x•x=-1×2⇒x=±1,故逆命题是假命题
解答 解:对于A,根据命题的否命题,既要否定条件,又要否定结论的原则,判定A正确;
对于B,∵存在实数使x2-x+1<1,∴命题“?x∈R,lg(x2-x+1)≥0”是假命题,故B正确;
对于C,由3sinx=$\sqrt{3}$得sinx∈[-1,1]得命题“?x∈R,3sinx=$\sqrt{3}$”是真命题,故C正确;
对于D,若向量$\overrightarrow{a}$=(-2x,1)与$\overrightarrow{b}$=(-2,x)共线⇒-2x•x=-1×2⇒x=±1,故逆命题是假命题,故D错
故选:D
点评 本题考查了命题真假判定,属于基础题.

练习册系列答案
相关题目
11.设直线l的方向向量为(1,-1,1),平面α的一个法向量为(-1,1,-1),则直线l与平面α的位置关系是( )
| A. | l?α | B. | l∥α | C. | l⊥α | D. | 不确定 |
18.过点M(-3,2),N(-2,3)的直线倾斜角是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
15.设实数x、y满足$\left\{\begin{array}{l}{y≤x}\\{x+y≤4}\\{y≥-2}\end{array}\right.$,则z=2x+y的最小值为( )
| A. | 6 | B. | 10 | C. | -6 | D. | -8 |
13.如果点P(sinθ,cosθ)位于第四象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
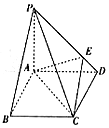 如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.
如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.