题目内容
9．过点（1，-2），且与两坐标轴都相切的圆的方程是x-5）2+（y+5）2=25或（x-1）2+（y+1）2=1．分析 由题意可得所求的圆的方程为 （x-a）2+（y+a）2=a2，a＞0，再把点（1，-2）代入，求得a的值，可得所求的圆的方程．
解答 解：由题意可得所求的圆在第四象限，设圆心为（a，-a），则半径为a，a＞0．
故圆的方程为（x-a）2+（y+a）2=a2，再把点（1，-2）代入，求得a=5或1，
故要求的圆的方程为（x-5）2+（y+5）2=25或（x-1）2+（y+1）2=1．
故答案为：（x-5）2+（y+5）2=25或（x-1）2+（y+1）2=1．
点评 本题主要考查用待定系数法求圆的标准方程的方法，求出圆心坐标和半径的值，是解题的关键，属于基础题．
练习册系列答案
相关题目
17．函数y=1-cos2x的定义域是（ ）
| A． | （-∞，0] | B． | [0，+∞） | C． | [-1，1] | D． | （-∞，+∞） |
14．已知α的终边和单位圆的交点坐标是（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$），则sin（$\frac{π}{2}$-α）cos（π+α）的值是（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | -$\frac{\sqrt{3}}{4}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
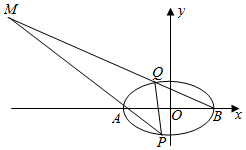已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{1}{3}$，且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$．
1．设集合M={x|x＜3}，N={x|x＞-1}，全集U=R，则∁U（M∩N）=（ ）
| A． | {x|x≤-1} | B． | {x|x≥3} | C． | {x|0＜x＜3} | D． | {x|x≤-1或x≥3} |