题目内容
 已知多面体ABCDE中,DE⊥平面ACD,AB∥DE,AC=AD=CD=DE=2,AB=1,O为CD的中点.
已知多面体ABCDE中,DE⊥平面ACD,AB∥DE,AC=AD=CD=DE=2,AB=1,O为CD的中点.(1)求证:AO∥平面BCE;
(2)求证:AO⊥平面CDE;
(3)求直线BD与平面BEC所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)利用线面平行的判定,先证明AO∥BF,∴AO∥平面BCE;
(2)先证明AO⊥CD,AO⊥DE,利用线面垂直的判定定理,可得AO⊥平面CDE;
(3)取CE中点F,连接BF,DF,证明DF⊥平面CBE,可得∠DBF就是求直线BD与平面BEC所成角,从而可得其正弦值.
(2)先证明AO⊥CD,AO⊥DE,利用线面垂直的判定定理,可得AO⊥平面CDE;
(3)取CE中点F,连接BF,DF,证明DF⊥平面CBE,可得∠DBF就是求直线BD与平面BEC所成角,从而可得其正弦值.
解答:
(1)证明:取CE中点F,连接BF,OF,∵O为CD的中点,
∴OF
DE,
∵AB∥DE,AC=AD=CD=DE=2,AB=1,∴OF
AB,
∴四边形ABFO为平行四边形,∴AO∥BF,
BF?面BCE,AO?面BCE,
∴AO∥平面BCE;
(2)证明:∵AC=AD,O为CD的中点,
∴AO⊥CD,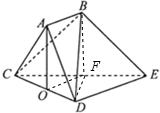
∵DE⊥平面ACD,AO?平面ACD,
∴AO⊥DE,
∵CD∩DE=D,
∴AO⊥平面CDE;
(3)解:取CE中点F,连接BF,DF,则AB∥DE且AB=
DE,
在△CDE中,OF∥DE且OF=
DE,
∴AB∥OF且AB=OF,
∴四边形ABFO是平行四边形,
∴BF∥AO,
∵AO⊥平面CDE,
∴BF⊥平面CDE,
∴BF⊥DF.
∵CD=DE,
∴DF⊥CE,
∵BF∩CE=F,
∴DF⊥平面CBE,
∴∠DBF就是求直线BD与平面BEC所成角.
在△BDF中,DF=
,BD=
,
∴sin∠DBF=
,
∴直线BD与平面BEC所成角的正弦值
.
∴OF
| ∥ |
. |
∵AB∥DE,AC=AD=CD=DE=2,AB=1,∴OF
| ∥ |
. |
∴四边形ABFO为平行四边形,∴AO∥BF,
BF?面BCE,AO?面BCE,
∴AO∥平面BCE;
(2)证明:∵AC=AD,O为CD的中点,
∴AO⊥CD,

∵DE⊥平面ACD,AO?平面ACD,
∴AO⊥DE,
∵CD∩DE=D,
∴AO⊥平面CDE;
(3)解:取CE中点F,连接BF,DF,则AB∥DE且AB=
| 1 |
| 2 |
在△CDE中,OF∥DE且OF=
| 1 |
| 2 |
∴AB∥OF且AB=OF,
∴四边形ABFO是平行四边形,
∴BF∥AO,
∵AO⊥平面CDE,
∴BF⊥平面CDE,
∴BF⊥DF.
∵CD=DE,
∴DF⊥CE,
∵BF∩CE=F,
∴DF⊥平面CBE,
∴∠DBF就是求直线BD与平面BEC所成角.
在△BDF中,DF=
| 2 |
| 5 |
∴sin∠DBF=
| ||
| 5 |
∴直线BD与平面BEC所成角的正弦值
| ||
| 5 |
点评:本题考查线面平行,线面垂直,考查线面角,考查学生分析解决问题的能力,正确作出线面角是关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
已知实数a在区间(0,2)上等可能随机取值,则函数f(x)=2x3-3ax2在区间(0,1)上有极小值的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知样本点(xi,yi)(i=1,2,…,n)的散点图呈线性正相关,且回归直线的斜率估计值的绝对值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
复数z=
的共轭复数是( )
| 1 |
| 1-i |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
