题目内容
设抛物线y2=2x，
（1）设点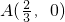
，求抛物线上距A最近的点P的坐标及相应的距离|PA|；
（2）设A（a，0）（a∈R），求在抛物线上一点到点A距离的最小值d，并写出函数式d=f（a）．
解：（1）设点P（x，y）是抛物线y2=2x上任意一点，
∴
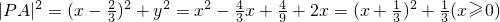
当x=0时，
，此时P（0，0）．
（2）设P（x，y）为y2=2x上任意一点，
∴|PA|2=（x-a）2+y2=x2-2ax+a2+2x=[x-（a-1）]2+2a-1（x≥0）
①当a≥1时，x=a-1≥0，即a≥1处|PA|小=
②当a＜1时，x=0，|PA|小=|a|
综上所述，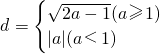
分析：（1）设P（x，y）为抛物线上任一点，进而根据勾股定理可得|PA|2=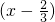
2+y2利用x的范围求得|PA|的范围
（2）依题意可得）|PA|2=（x-a）2+y2=分析当a-1≥0和a-1＜0时|PA|的最小值，进而可求得d．
点评：本题主要考查抛物线的性质，综合了函数的定义域和值域的问题，要注意对a的范围进行分类讨论，属于中档题．
∴
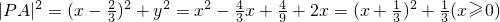
当x=0时，
，此时P（0，0）．（2）设P（x，y）为y2=2x上任意一点，
∴|PA|2=（x-a）2+y2=x2-2ax+a2+2x=[x-（a-1）]2+2a-1（x≥0）
①当a≥1时，x=a-1≥0，即a≥1处|PA|小=
②当a＜1时，x=0，|PA|小=|a|
综上所述，
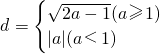
分析：（1）设P（x，y）为抛物线上任一点，进而根据勾股定理可得|PA|2=
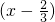2+y2利用x的范围求得|PA|的范围（2）依题意可得）|PA|2=（x-a）2+y2=分析当a-1≥0和a-1＜0时|PA|的最小值，进而可求得d．
点评：本题主要考查抛物线的性质，综合了函数的定义域和值域的问题，要注意对a的范围进行分类讨论，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设抛物线y2=2x的焦点为F，过点M（
，0）的直线与抛物线相交于A、B两点，与抛物线的准线相交于点C，|BF|=2，则△BCF与△ACF的面积之比
=（ ）
| 3 |
| S△BCF |
| S△ACF |
A、
| ||
B、
| ||
C、
| ||
D、
|
设抛物线y2=2x，线段AB的两个端点在抛物线上，且|AB|=3，那么线段AB的中点M到y轴的最短距离是（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |