Question

设抛物线y²=2x的焦点为F，过点M（

3

，0）的直线与抛物线相交于A，B两点，与抛物线的准线相交于C，|BF|=2，则

|BC|

|AC|

=（　　）

• A．

  4

  5

• B．

  2

  3

• C．

  4

  7

• D．

  1

  2

Answer 1

分析：过A、B作抛物线准线的垂线，垂足分别为D、E，连结AD、BE、AF．设A（x₁，y₁）、B（x₂，y₂），直线AB的方程为y=k（x-

3

），将AB方程与抛物线方程消去y得到关于x的一元二次方程，由韦达定理算出x₁x₂=3．利用抛物线的定义得|BF|=|BE|=x₂+

1

2

=2，算出x₂=

3

2

，从而得出x₁=2，可得|AD|=x₁+

1

2

=

5

2

．最后在△CAD中根据平行线的性质加以计算，即可得到

|BC|

|AC|

的值．

解答：解：抛物线y²=2x的焦点为F（

1

2

，0），准线方程为x=-

1

2

，
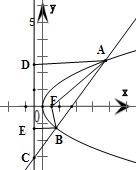
分别过A、B作准线的垂线，垂足分别为D、E，连结AD、BE、AF．
设A（x₁，y₁）、B（x₂，y₂），直线AB的方程为y=k（x-

3

），与y²=2x消去y，
得k²x²-（2+2

3

k²）x+3k²=0，所以x₁+x₂=

2+2 3 k2

k2

，x₁x₂=3，
∵|BF|=2，∴根据抛物线的定义，得|BF|=|BE|=x₂+

1

2

=2，解得x₂=

3

2

．
由此可得x₁=

3

x2

=2，所以|AD|=x₁+

1

2

=

5

2

，
∵△CAD中，BE∥AD，∴

|BC|

|AC|

=

|BE|

|AD|

=

2

5 2

=

4

5

．
故选：A

点评：本题给出抛物线与经过M（

3

，0）的直线相交，求截得的线段之间的比值．着重考查了抛物线的定义与简单几何性质、直线与抛物线的位置关系等知识，属于中档题．