题目内容
1.已知在四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,AB⊥AD,BC∥AD,且AB=2,AD=4,BC=1,侧棱AA1=4.(1)若E为AA1上一点,试确定E点的位置,使EB∥平面A1CD;
(2)在(1)的条件下,求二面角E-BD-A的余弦值.
分析 (1)以AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出当E点的坐标为(0,0,3),${A_1}E=\frac{1}{4}{A_1}A$时,EB∥平面A1CD.
(2)连接ED,BD,AA1求出平面ABD的一个法向量和平面BED的一个法向量,利用向量法能求出二面角E-BD-A的余弦值.
解答 解:(1)当${A_1}E=\frac{1}{4}{A_1}A$时,EB∥平面A1CD.
如图,以AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
连接EB,则A(0,0,0),B(2,0,0),D(0,4,0),
C(2,1,0),A1(0,0,4).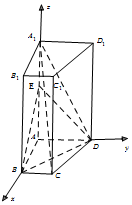 设E(0,0,z),则$\overrightarrow{BE}=({-2,0,z})$,$\overrightarrow{C{A_1}}=({-2,-1,4})$,$\overrightarrow{CD}=({-2,3,0})$.∵$EB\user1{∥}$平面A1CD,
设E(0,0,z),则$\overrightarrow{BE}=({-2,0,z})$,$\overrightarrow{C{A_1}}=({-2,-1,4})$,$\overrightarrow{CD}=({-2,3,0})$.∵$EB\user1{∥}$平面A1CD,
∴不妨设$\overrightarrow{BE}=x\overrightarrow{CA}+y\overrightarrow{CD}$,
∴(-2,0,z)=x(-2,-1,4)+y(-2,3,0).
∴$\left\{\begin{array}{l}-2=-2x-2y\\ 0=-x+3y\\ z=4x\end{array}\right.$,解得z=3.
所以当E点的坐标为(0,0,3),${A_1}E=\frac{1}{4}{A_1}A$时,EB∥平面A1CD.
(2)连接ED,BD,AA1⊥平面ABD,
∴向量$\vec m=({0,0,1})$为平面ABD的一个法向量.
设平面BED的一个法向量为$\vec n=({{x_0},{y_0},1})$,
而$\overrightarrow{BE}=({-2,0,3})$,$\overrightarrow{BD}=({-2,4,0})$,
∴$\left\{\begin{array}{l}\vec n•\overrightarrow{BE}=-2{x_0}+3=0\\ \vec n•\overrightarrow{BD}=-2{x_0}+4{y_0}=0\end{array}\right.$,解得$\vec n=({\frac{3}{2},\frac{3}{4},1})$.
∴$cos\left?{m,n}\right>=\frac{\vec m•\vec n}{{|{\vec m}|•|{\vec n}|}}$=$\frac{1}{{1×\sqrt{{{({\frac{3}{2}})}^2}+{{({\frac{3}{4}})}^2}+{1^2}}}}$=$\frac{{4\sqrt{61}}}{61}$.
所以二面角E-BD-A的余弦值为$\frac{{4\sqrt{61}}}{61}$.
点评 本题考查二面角的余弦值的求法,考查满足线面平行的点是否存在的求法与判断,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、转化化归思想,是中档题.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案(1)根据以上数据建立一个2×2的列联表;
(2)判断是否能有95%的把握说晕机与性别有关?
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 3 个 | B. | 2 个 | C. | 1个 | D. | 0个 |
 某几何体的三视图如图所示,则下列说法正确的是( )
某几何体的三视图如图所示,则下列说法正确的是( )①该几何体的体积为$\frac{1}{6}$;
②该几何体为正三棱锥;
③该几何体的表面积为$\frac{3}{2}$+$\sqrt{3}$;
④该几何体外接球的表面积为3π
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
| A. | $A_{2n}^n$ | B. | n2n | C. | (2n)n | D. | ${C}_{2n}^{n}$ |
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,与x轴交于A、B两点,与y轴交于P点,其一条对称轴与x轴交于C点,且PA=PC=2$\sqrt{3}$,PB=BC.则ω=$\frac{π}{4}$.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,与x轴交于A、B两点,与y轴交于P点,其一条对称轴与x轴交于C点,且PA=PC=2$\sqrt{3}$,PB=BC.则ω=$\frac{π}{4}$.