题目内容
已知t∈R，圆C：x2＋y2－2tx－2t2y＋4t－4＝0.
(1) 若圆C的圆心在直线x－y＋2＝0上，求圆C的方程；
(2) 圆C是否过定点？如果过定点，求出定点的坐标；如果不过定点，说明理由．
解：(1) 配方得(x－t)2＋(y－t2)2＝t4＋t2－4t＋4，其圆心C(t，t2)．依题意t－t2＋2＝0t＝－1或2.
即x2＋y2＋2x－2y－8＝0或x2＋y2－4x－8y＋4＝0为所求方程．
(2) 整理圆C的方程为(x2＋y2－4)＋(－2x＋4)t＋(－2y)·t2＝0，令
故圆C过定点(2，0)．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
的是（ ）
B．
D．
互相垂直，则m的值为（ ）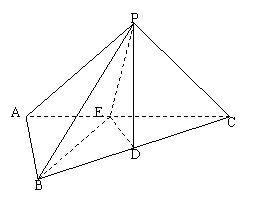
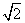.求动点M的轨迹方程，并说明它表示什么．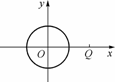
中，
，
分别是
及
的中点，
是
的中点，沿
，
及
，
，
折起使
，
，
三点重合，重合后的点记作
，那么在四面体
中必有（ ）
面
Ｂ.
面
Ｃ.
面
面
在区间
内围成图形的面积为：（ ）
B．
C．
D．
＞