题目内容
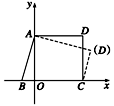
已知A(0,3)、B(-1,0)、C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).
使ABCD为直角梯形的点D的坐标可以为(3,3)或![]()
解析:
设所求点D的坐标为(x,y),如图所示,由于kAB=3,kBC=0,
∴kAB·kBC=0≠-1,
即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角边.
(1)若CD是直角梯形的直角边,则BC⊥CD,AD⊥CD,
∵kBC=0,∴CD的斜率不存在,从而有x=3.
又kAD=kBC,∴![]() =0,即y=3.
=0,即y=3.
此时AB与CD不平行.
故所求点D的坐标为(3,3).
(2)若AD是直角梯形的直角边,
则AD⊥AB,AD⊥CD,
kAD=![]() ,kCD=
,kCD=![]() .
.
由于AD⊥AB,∴![]() ·3=-1.
·3=-1.
又AB∥CD,∴![]() =3.
=3.
解上述两式可得![]()
此时AD与BC不平行.
故所求点D的坐标为![]() ,
,
综上可知,使ABCD为直角梯形的点D的坐标可以为(3,3)或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A(0,-3),B(3,3),C(x,-1),若
与
共线,则x等于( )
| AB |
| BC |
| A、5 | B、1 | C、-1 | D、-5 |