Question

已知A（0，3），B（-1，0），C（3，0），求D点的坐标，使四边形ABCD为直角梯形（A，B，C，D按逆时针方向排列）．

Answer 1

分析：根据题目给出的条件画出图形，由图形直观看出四边形只有边CD和AD垂直时才能构成直角梯形，然后借助于向量数量积为0及模的长度列式求解．

解答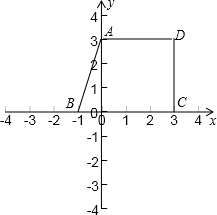：解：如图，A（0，3），B（-1，0），C（3，0），要使四边形ABCD为直角梯形（A，B，C，D按逆时针方向排列），
若D点为图示情况，设D（x，y），

AD

=(x，y-3)，

CD

=(x-3，y)，
由四边形ABCD为直角梯形，得：

AD

•

CD

=0，且|

OD

|=3

2

．
即x（x-3）+y（y-3）=0①，且

x2+y2

=3

2

②．
联立①②解得：x=y=3．
所以，使四边形ABCD为直角梯形（A，B，C，D按逆时针方向排列）的D点的坐标为（3，3）．
若AD⊥AB，则AD所在直线方程为y=-

1

3

x+3，CD所在直线方程为y=3x-9，联立解得D（

18

5

，

9

5

）．

点评：本题考查了向量的数量积判断两个向量的垂直关系，考查了数形结合的解题思想，考查了计算能力，是基础题．