题目内容
4.已知a>0,b>0,则“log2a>log2b”是“${({\frac{1}{3}})^a}<{({\frac{1}{3}})^b}$”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据指数函数以及对数函数的性质结合充分必要条件的定义判断即可.
解答 解:∵a>0,b>0,
∴log2a>log2b?a>b?${({\frac{1}{3}})^a}<{({\frac{1}{3}})^b}$,
故选:C.
点评 本题考查了指数函数、对数函数的性质,考查充分必要条件,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若x,y满足$\left\{\begin{array}{l}{x+y≥0}\\{x≥1}\\{x-y≥0}\end{array}\right.$,则下列不等式恒成立的是( )
| A. | y≥0 | B. | x≥2 | C. | 2x-y+1≥0 | D. | x+2y+1≥0 |
15.若实数x,y满足约束条件$\left\{\begin{array}{l}x-y-1≤0\\ x+3≥0\\ y-2≤0\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -8 | B. | -6 | C. | -2 | D. | 4 |
14.已知角α的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边经过点P(1,-2),则sin2α=( )
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
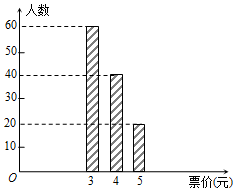 已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示. 已知定直线l:y=x+3,定点A(2,1),以坐标轴为对称轴的椭圆C过点A且与l相切.
已知定直线l:y=x+3,定点A(2,1),以坐标轴为对称轴的椭圆C过点A且与l相切.