题目内容
20.已知直线y=kx+1,当k变化时,此直线被椭圆$\frac{{x}^{2}}{4}$+y2=1截得的最大弦长是( )| A. | 4 | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 直线y=kx+1恒过定点P(0,1),且是椭圆的短轴上顶点,因而此直线被椭圆截得的弦长,即为点P与椭圆上任意一点Q的距离,设椭圆上任意一点Q(2cosθ,sinθ),利用三角函数即可得到结论.
解答 解:直线y=kx+1恒过定点P(0,1),且是椭圆的短轴上顶点,
因而此直线被椭圆截得的弦长,即为点P与椭圆上任意一点Q的距离,
设椭圆上任意一点Q(2cosθ,sinθ)
∴|PQ|2=(2cosθ)2+(sinθ-1)2=-3sin2θ-2sinθ+5,
∴当sinθ=-$\frac{1}{3}$时,|PQ|2max=$\frac{16}{3}$,
∴直线被椭圆$\frac{{x}^{2}}{4}$+y2=1截得的最大弦长|PQ|max=$\frac{4\sqrt{3}}{3}$.
故选:B.
点评 本题考查直线与椭圆的位置关系,考查三角函数知识,解题的关键是将问题转化为点P与椭圆上任意一点Q的距离的最大值.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
11.设a,b,c大于0,则3个数:$a+\frac{1}{b}$+1,$b+\frac{1}{c}$+1,$c+\frac{1}{a}$+1的值( )
| A. | 都大于3 | B. | 至多有一个不大于3 | ||
| C. | 都小于3 | D. | 至少有一个不小于3 |
10.在△ABC中,角A,B,C所对的边分别为a,b,c,若b=2$\sqrt{3}$.B=120°,C=30°,则a=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
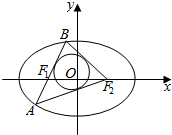 如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.
如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.