题目内容
13.若6x2+4y2+6xy=1,x,y∈R,则x2-y2的最大值为$\frac{1}{5}$.分析 令x2-y2=t,条件式两边同乘t,得到关于$\frac{x}{y}$的方程,根据方程有解列不等式得出t的范围.
解答 解:设x2-y2=t,
则6tx2+4ty2+6txy=x2-y2,
即(6t-1)x2+6txy+(4t+1)y2=0,
若y=0,则x2=$\frac{1}{6}$,此时t=$\frac{1}{6}$,
若y≠0,则(6t-1)($\frac{x}{y}$)2+6t•$\frac{x}{y}$+(4t+1)=0有解
∴6t-1=0或36t2-4(6t-1)(4t+1)≥0,
解得-$\frac{1}{3}$≤t≤$\frac{1}{5}$,
当且仅当x+3y=0且y2=$\frac{1}{40}$时,t取得最大值$\frac{1}{5}$.
故答案为$\frac{1}{5}$.
点评 本题考查了二次函数的性质,属于中档题.

练习册系列答案
相关题目
5.给定R上的函数f(x),( )
| A. | 存在R上函数g(x),使得f(g(x))=x | B. | 存在R上函数g(x),使得g(f(x))=x | ||
| C. | 存在R上函数g(x),使得f(g(x))=g(x) | D. | 存在R上函数g(x),使得f(g(x))=g(f(x)) |
18.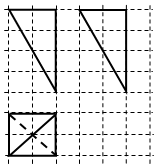 如图是某几何体的三视图,图中方格的单位长度为1,则该几何体外接球的直径为( )
如图是某几何体的三视图,图中方格的单位长度为1,则该几何体外接球的直径为( )
 如图是某几何体的三视图,图中方格的单位长度为1,则该几何体外接球的直径为( )
如图是某几何体的三视图,图中方格的单位长度为1,则该几何体外接球的直径为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | 4 |
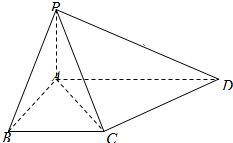 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=$\frac{1}{2}$AD.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=$\frac{1}{2}$AD.