Question

1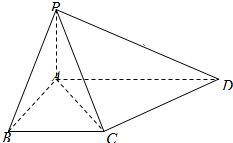．如图，四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB，底面ABCD为直角梯形，∠ABC=∠BAD=90°，PA=BC=$\frac{1}{2}$AD．
（1）求证：CD⊥平面PAC；
（2）在棱PD上是否存在一点E，使CE∥平面PAB？若存在，指出E的位置；若不存在，说明理由．

Answer 1

分析 （1）设PA=1，由勾股定理逆定理得AC⊥CD，根据线面垂直的性质可知PA⊥CD，又PA∩AC=A，根据线面垂直的判定定理可知CD⊥面PAC，
（2）在棱PD上存在一点E，E为PD中点，使CE∥平面PAB，取AD的中点为F．连接EF，CF．由题设条件推导出EF∥PA，CF∥AB，得到面EFC∥面PAB，由此能够证明CE∥面PAB．

解答 解：（1）证明：设PA=1．
由题意PA=BC=1，AD=2．
∵AB=1，BC=$\frac{1}{2}$，由∠ABC=∠BAD=90°．易得CD=AC=$\sqrt{2}$．
由勾股定理逆定理得AC⊥CD．
又∵PA⊥面ABCD，CD?面ABCD，
∴PA⊥CD．又PA∩AC=A，∴CD⊥面PAC．
（2）在棱PD上存在一点E，E为PD中点，使CE∥平面PAB
理由：取AD的中点F．连接EF，CF．
∵PA⊥面ABCD．底面ABCD为直角梯形，∠ABC=∠BAD=90°，BC=$\frac{1}{2}$AD，E为PD的中点．
∴EF∥PA，CF∥AB，
∴面EFC∥面PAB，
所以CE∥面PAB．∴棱PD上存在一点E，E为PD中点，使CE∥平面PAB．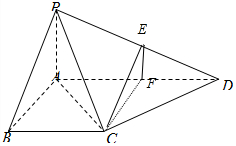

点评 本小题主要考查空间中的线面关系，考查线面平行、面面垂直的判定，考查空间想象能力和推理论证能力，考查转化思想，属于中档题．