题目内容
10.(1)求值sin34°sin26°-sin56°cos26°;(2)化简sin50°($\sqrt{3}$tan10°+1)
分析 (1)利用诱导公式,两角和的余弦函数公式化简,根据特殊角的三角函数值即可求值得解.
(2)利用同角三角函数基本关系式,两角和的正弦函数公式,倍角公式,诱导公式化简即可求值得解.
解答 (本题满分为12分)
解:(1)sin34°sin26°-sin56°cos26°
=sin34°sin26°-cos34°cos26°
=-(cos34°cos26°-sin34°sin26°)
=-cos(34°+26°)
=-cos60°
=-$\frac{1}{2}$…(6分)
(2)sin50°($\sqrt{3}$tan10°+1)
=sin50°($\sqrt{3}$$\frac{sin10°}{cos10°}$+1)
=sin50°($\frac{\sqrt{3}sin10°+cos10°}{cos10°}$)
=sin50°•$\frac{2[\frac{\sqrt{3}}{2}sin10°+\frac{1}{2}cos10°]}{cos10°}$
=$\frac{2sin50°sin40°}{cos10°}$
=$\frac{2sin40°cos40°}{cos10°}$
=$\frac{sin80°}{cos10°}$
=1…(12分)
点评 本题考查三角函数的求值,考查同角三角函数基本关系式,两角和差的余弦公式、二倍角的正弦公式和诱导公式的运用,考查角的变换技巧,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=4,$\overrightarrow{a}$•$\overrightarrow{b}$=-10,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
14.已知$\overrightarrow a,\overrightarrow b$是单位向量,$\overrightarrow a•\overrightarrow b=0$,若向量c满足$|{\overrightarrow c-\overrightarrow a+\overrightarrow b}$|=1,则|$|{\overrightarrow c-\overrightarrow b}$|的取值范围是( )
| A. | $[{\sqrt{2}-1,\sqrt{2}+1}]$ | B. | $[{1,\sqrt{2}+1}]$ | C. | [0,2] | D. | $[{\sqrt{5}-1,\sqrt{5}+1}]$ |
 是
是 的直径,
的直径,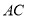 是
是 的切线,
的切线, 交
交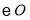 于点
于点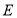 .
.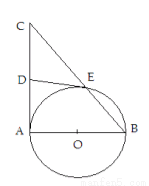
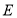 做
做 的切线,交
的切线,交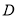 ,证明:
,证明: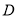 是
是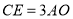 ,求
,求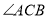 的大小.
的大小.