题目内容
8.已知函数f(x)=|x2-2ax+b|(x∈R),给出下列命题:①?a∈R,使f(x)为偶函数;
②若f(0)=f(2),则f(x)的图象关于x=1对称;
③若a2-b≤0,则f(x)在区间[a,+∞)上是增函数;
④若a2-b-2>0,则函数h(x)=f(x)-2有2个零点.
其中正确命题的序号为①③.
分析 ①当a=0时,f(x)=|x2+b|显然是偶函数,故①正确;
②由f(0)=f(2),则|b|=|4-4a+b|,取a=0,b=-2,此式成立,此时函数化为f(x)=|x2-2|,其图象不关于x=1对称,故②错误;
③f(x)=|(x-a)2+b-a2|=(x-a)2+b-a2在区间[a,+∞)上是增函数,故③正确;
④画出图象可知,h(x)=|(x-a)2+b-a2|-2有4个零点,故④错误.
解答 解:①当a=0时,f(x)=|x2+b|显然是偶函数,故①正确;
②取a=0,b=-2,函数f(x)=|x2-2ax+b|化为f(x)=|x2-2|,满足f(0)=f(2),
但f(x)的图象不关于x=1对称,故②错误;
③若a2-b≤0,则f(x)=|(x-a)2+b-a2|=(x-a)2+b-a2在区间[a,+∞)上是增函数,故③正确;
④h(x)=|(x-a)2+b-a2|-2有4个零点,故④错误.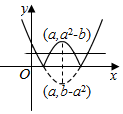
∴正确命题为①③.
故答案为:①③.
点评 本题考查了命题的真假判断与应用,考查了二次函数的性质,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知集合A={x|x>1|},B={x|$\frac{1}{x}$<1},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.若集合A={-3,-1,0,2,4},集合B={x|x>log23},则A∩(∁RB)等于( )
| A. | {2,4} | B. | {-3,-1} | C. | {-3,-1,0} | D. | {0,2,4} |
13.下列函数中,值域是(0,+∞)的是( )
| A. | y=($\frac{1}{3}$)1-x | B. | y=x2 | C. | y=5${\;}^{\frac{1}{2-x}}$ | D. | y=$\sqrt{1-{2}^{x}}$ |