题目内容
已知整数数集 A={a1,a2,a3,…,an}(a1<a2<a3<…<an,n≥3)具有性质 P:对任意i,j,k(1≤i<j<k),ai+ak-aj∈A.
(Ⅰ)请举出一个满足上述条件且含有5个元素的数集 A;
(Ⅱ)求证:a1,a2,a3,…,an是等差数列;
(Ⅲ)已知a1=2,an=2015,且20∈A⊆N,求数集 A中所有元素的和的最小值.
(Ⅰ)请举出一个满足上述条件且含有5个元素的数集 A;
(Ⅱ)求证:a1,a2,a3,…,an是等差数列;
(Ⅲ)已知a1=2,an=2015,且20∈A⊆N,求数集 A中所有元素的和的最小值.
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(Ⅰ)5个元素能构成等差数列即可;
(Ⅱ)ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,可得ak+1=ak+ak+2-ak+1,即可证明结论;
(Ⅲ)由(Ⅱ)可知,2,a2,a3,…,2015是等差数列,确定d是18和2013的公约数,利用求和公式,即可得出结论.
(Ⅱ)ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,可得ak+1=ak+ak+2-ak+1,即可证明结论;
(Ⅲ)由(Ⅱ)可知,2,a2,a3,…,2015是等差数列,确定d是18和2013的公约数,利用求和公式,即可得出结论.
解答:
(Ⅰ)解:由题意A={1,2,3,4,5};
(Ⅱ)证明:对任意k+2≤n,由性质P可得ak+ak+2-ak+1∈A,
∵ak<ak+1<ak+2,
∴ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,
∴ak+1=ak+ak+2-ak+1,
∴2ak+1=ak+ak+2,
∴a1,a2,a3,…,an是等差数列;
(Ⅲ)解:由(Ⅱ)可知,2,a2,a3,…,2015是等差数列,
不妨设公差为d,ak=20,
则20-2=(k-1)d,2015-2=(n-1)d,
∵A⊆N,
∴d是18和2013的公约数,
由等差数列求和公式可得Sn=
×n=
×(
+1),
∴d越大,Sn越小,
∴d为18和2013的最大公约数3时,Sn最小,最小为677712.
(Ⅱ)证明:对任意k+2≤n,由性质P可得ak+ak+2-ak+1∈A,
∵ak<ak+1<ak+2,
∴ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,
∴ak+1=ak+ak+2-ak+1,
∴2ak+1=ak+ak+2,
∴a1,a2,a3,…,an是等差数列;
(Ⅲ)解:由(Ⅱ)可知,2,a2,a3,…,2015是等差数列,
不妨设公差为d,ak=20,
则20-2=(k-1)d,2015-2=(n-1)d,
∵A⊆N,
∴d是18和2013的公约数,
由等差数列求和公式可得Sn=
| 2+2015 |
| 2 |
| 2+2015 |
| 2 |
| 2013 |
| d |
∴d越大,Sn越小,
∴d为18和2013的最大公约数3时,Sn最小,最小为677712.
点评:本题考查数列的应用,考查学生对新定义的理解,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数y=f(x)在x=x0处可导,若
=-
,则f′(x0)等于( )
| lim |
| k→0 |
| f(x0-k)-f(x0) |
| 2k |
| 1 |
| 4 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
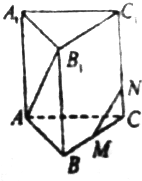 正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.
正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.