题目内容
已知函数f(x)=x-2+
(x>1),当x=a时,取f(x)的最小值b,则a+b=( )
| 1 |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
考点:基本不等式
专题:不等式的解法及应用
分析:把函数解析式转化成x-1+
-1利用基本不等式求得起最小值b,同时根据等号成立的条件求得a,最后求得a+b.
| 1 |
| x-1 |
解答:
解:∵x>1,
∴x-1>0,
∴f(x)=x-2+
=x-1+
-1≥2-1=1,当且仅当x-1=
,即x=2时等号成立,
∴a=2,b=1,
∴a+b=3,
故选C.
∴x-1>0,
∴f(x)=x-2+
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
∴a=2,b=1,
∴a+b=3,
故选C.
点评:本题主要考查了基本不等式的应用.在应用基本不等式时,注意条件的满足.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知实数x,y满足
,则不等式2|1-a|-1>a(a-2)成立的概率是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
在锐角△ABC中,C=
,则tanA+tanB的最小值为( )
| π |
| 4 |
A、3+2
| ||
B、2+2
| ||
C、2
| ||
D、2
|
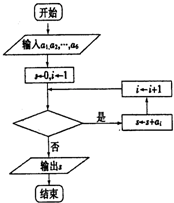 如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填( )
如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填( )| A、i≤5或i<6 |
| B、i≤6或i<7 |
| C、i≥6或i>5 |
| D、i≥5或i>4 |
设θ是△ABC的一个内角,且sinθ+cosθ=
,则x2sinθ+y2cosθ=1表示( )
| 1 |
| 5 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
y=
x2-ln(2x-3)的单调递减区间为( )
| 1 |
| 2 |
A、(-∞,-
| ||
| B、(2,+∞) | ||
C、(
| ||
D、(
|
已知f(x)的图象与函数y=log3(x-1)+9的图象关于直线y=x对称,则f(10)的值为( )
| A、11 | B、12 | C、2 | D、4 |
过双曲线x2-y2=4的左焦点F1有一条弦PQ在左支上,若|PQ|=7,F2是双曲线的右焦点,则△PF2Q的周长是( )
| A、8 | B、15 | C、26 | D、22 |
过点P(12,0)且与y轴相切于原点的圆的方程为( )
| A、(x+6)2+y2=36 |
| B、x2+(y+6)2=36 |
| C、(x-6)2+y2=36 |
| D、x2+(y-6)2=36 |