题目内容
取棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,依次进行下去,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则此多面体:①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
a3. 以上结论正确的是( )
| 5 |
| 6 |
| A、①②⑤ | B、①②③ |
| C、②④⑤ | D、②③④⑤ |
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:先根据题意画出图形,如图,原来的六个面还在只不过是变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,计算或数一数它的面数等,再结合割补法求出它的表面积及体积即可.
解答:
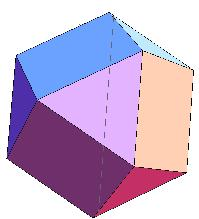 解:如图,原来的六个面还在只不过是变成了一个小正方形,
解:如图,原来的六个面还在只不过是变成了一个小正方形,
再添了八个顶点各对应的一个三角形的面,
所以总计6+8=14个面,故③错;
每个正方形4条边,每个三角形3条边,4×6+3×8=48,
考虑到每条边对应两个面,所以实际只有
×48=24条棱.②正确;
所有的顶点都出现在原来正方体的棱的中点位置,
原来的棱的数目是12,所以现在的顶点的数目是12.
或者从图片上可以看出每个顶点对应4条棱,
每条棱很明显对应两个顶点,
所以顶点数是棱数的一半即12个.①正确;
三角形和四边形的边长都是
a,所以正方形总面积为6×
a2=3a2,
三角形总面积为8×
×
a2sin60°=
a2,
表面积(3+
)a2,故④错;
体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×
(
)3=
a2,
剩余总体积为a3-
a3=
a3.⑤正确.
故选:A.
 解:如图,原来的六个面还在只不过是变成了一个小正方形,
解:如图,原来的六个面还在只不过是变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,
所以总计6+8=14个面,故③错;
每个正方形4条边,每个三角形3条边,4×6+3×8=48,
考虑到每条边对应两个面,所以实际只有
| 1 |
| 2 |
所有的顶点都出现在原来正方体的棱的中点位置,
原来的棱的数目是12,所以现在的顶点的数目是12.
或者从图片上可以看出每个顶点对应4条棱,
每条棱很明显对应两个顶点,
所以顶点数是棱数的一半即12个.①正确;
三角形和四边形的边长都是
| ||
| 2 |
| 1 |
| 2 |
三角形总面积为8×
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
表面积(3+
| 3 |
体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×
| 1 |
| 6 |
| a |
| 2 |
| 1 |
| 6 |
剩余总体积为a3-
| 1 |
| 6 |
| 5 |
| 6 |
故选:A.
点评:本小题主要考查棱柱的结构特征、多面体的表面积与体积等基础知识,考查运算求解能力,考查空间想象能力、化归与转化思想.属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
已知函数f(x)=(
)x-log2x,若x0是函数y=f(x)的零点,且0<x1<x0,则有( )
| 1 |
| 3 |
| A、f(x1)>0 |
| B、f(x1)<0 |
| C、f(x1)=0 |
| D、f(x1)>0与f(x1)<0均有可能 |
已知函数y=ax2(x≠0)在点(1,a)处切线的倾斜角是45°,则a的值是( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
设p、q是简单命题,则“p∧q为真”是“p∨q为真”的( )
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知数列{an}中,an=n2-n-50,则-8是它的第几项( )
| A、5项 | B、6项 | C、7项 | D、8项 |
如图程序运行后输出的结果为( )


| A、10 | B、9 | C、6 | D、5 |
已知双曲线中心在原点,且一个焦点为F(3,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为-1,则双曲线的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若S={1,2,3,4,5},M={1,3,4},N={2,4,5},则(∁SM)∩(∁SN)等于( )
| A、{1,3} | B、∅ |
| C、{4} | D、{2,5} |