题目内容
2.将函数y=sin(ωx-$\frac{π}{6}$)(ω>0)的图象向左平移$\frac{π}{3ω}$个单位,得到函数f(x)的图象,若函数f(x)在(0,2]上恰有一个最大值1和最小值-1,则ω的取值范围是$\frac{2π}{3}$≤ω<$\frac{7π}{6}$.分析 根据三角函数的图象变换关系,先求出函数f(x)的解析式,然后求出ωx+$\frac{π}{6}$的取值范围,利用数形结合进行求解即可.
解答 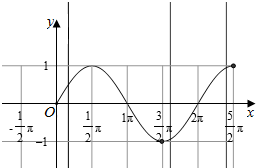 解:y=sin(ωx-$\frac{π}{6}$)(ω>0)的图象向左平移$\frac{π}{3ω}$个单位,
解:y=sin(ωx-$\frac{π}{6}$)(ω>0)的图象向左平移$\frac{π}{3ω}$个单位,
得到y=sin[ω(x+$\frac{π}{3ω}$)-$\frac{π}{6}$]=sin(ωx+$\frac{π}{6}$),
即f(x)=sin(ωx+$\frac{π}{6}$),
当0<x≤2时,$\frac{π}{6}$<ωx+$\frac{π}{6}$≤2ω+$\frac{π}{6}$,
要使函数f(x)在(0,2]上恰有一个最大值1和最小值-1,
则$\frac{3π}{2}$≤2ω+$\frac{π}{6}$<$\frac{5π}{2}$,
即$\frac{8π}{6}$≤2ω<$\frac{14π}{6}$,
即即$\frac{2π}{3}$≤ω<$\frac{7π}{6}$,
故答案为:$\frac{2π}{3}$≤ω<$\frac{7π}{6}$.
点评 本题主要考查三角函数的图象和性质,根据条件求出函数的解析式,利用三角函数的图象和性质建立不等式关系是解决本题的关键.综合性较强.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13.在底面直径和高均为4的圆柱体内任取一点P,则点P到该圆柱体上、下底面圆心的距离均不小于2的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
10.四棱锥的8条棱分别代表8种不同的国家级保护动物,有公共点的2条棱所代表的2种动物不能放在同一放养区,没有公共的点的2条棱所代表的2种动物可以放在同一放养区,现打算用编号a,b,c,d的4个放养区来放养这8种动物,那么安全的放养方式有( )
| A. | 96种 | B. | 48种 | C. | 24种 | D. | 100种 |
17.已知函数f(x+2)是偶函数,且当x>2时满足xf′(x)>2f′(x)+f(x),则( )
| A. | 2f(1)<f(4) | B. | 2f($\frac{3}{2}$)<f(4) | C. | f(0)<4f($\frac{5}{2}$) | D. | f(1)<f(3) |
7.已知函数f(x)=ax+b是奇函数,且过点(4,-12),则a、b的值分别为( )
| A. | a=0,b=-3 | B. | a=-3,b=0 | C. | a=3,b=0 | D. | a=0,b=3 |