题目内容
13.已知椭圆C经过点A(2,3),且点F(2,0)为其右焦点,则椭圆C的标准方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1.分析 设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=2,结合a,b,c的关系和点A(2,3),代入椭圆方程,解方程可得a,b,进而得到椭圆方程.
解答 解:设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=2,即有a2-b2=4,
代入点A(2,3),可得$\frac{4}{{a}^{2}}$+$\frac{9}{{b}^{2}}$=1,
解得a=4,b=2$\sqrt{3}$.
即有椭圆方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1.
故答案为:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1.
点评 本题考查椭圆的方程的求法,注意运用待定系数法,考查运算能力,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
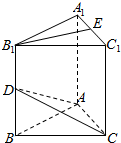 如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.
如图在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\frac{1}{2}$AA1,∠BAC=90°,点D,E分别为棱BB1,A1C1的中点,求异面直线B1E、CD所成角的余弦值.