题目内容
20.若不等式组$\left\{{\begin{array}{l}{x+3y-4≥0}\\{3x+y-4≤0}\\{x≥0}\end{array}}\right.$所表示的平面区域被直线y=kx+$\frac{4}{3}$分为面积相等的两部分,则k的值是( )| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 由约束条件作出可行域,由直线y=kx+$\frac{4}{3}$过点A(0,$\frac{4}{3}$),结合平面区域被直线y=kx+$\frac{4}{3}$分为面积相等的两部分,可知直线过B,C的中点D,求出D的坐标,利用两点求斜率公式得答案.
解答 解:由约束条件$\left\{{\begin{array}{l}{x+3y-4≥0}\\{3x+y-4≤0}\\{x≥0}\end{array}}\right.$作出可行域如图,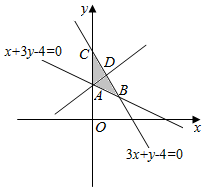
A(0,$\frac{4}{3}$),C(0,4),
联立$\left\{\begin{array}{l}{3x+y-4=0}\\{x+3y-4=0}\end{array}\right.$,解得B(1,1),
直线y=kx+$\frac{4}{3}$过定点A(0,$\frac{4}{3}$),
要使平面区域被直线y=kx+$\frac{4}{3}$分为面积相等的两部分,
则直线y=kx+$\frac{4}{3}$过BC的中点D,
由中点坐标公式D($\frac{1}{2}$,$\frac{5}{2}$),
∴$k={k}_{AD}=\frac{\frac{5}{2}-\frac{4}{3}}{\frac{1}{2}-0}=\frac{7}{3}$.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.执行如图所示的程序框图,若输入x=1,则输出y的值是( )
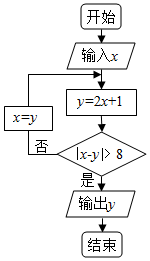

| A. | 7 | B. | 15 | C. | 23 | D. | 31 |
5.已知函数f(x)=$\left\{\begin{array}{l}{x+1,0≤x<1}\\{{2}^{x-1}-1,1≤x<3}\end{array}\right.$,若存在m,n,当0≤m<n<3时,有f(m)=f(n),则nf(m)的取值范围是( )
| A. | [1,3) | B. | [1,2log23+2) | C. | [2,3) | D. | [2,2log23+2) |
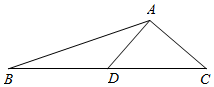 已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.
已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.