题目内容
13．过点（0，2）且与两坐标轴相切的圆的标准方程为（x-2）2+（y-2）2=4或（x+2）2+（y-2）2=4．分析 由题意可得所求的圆心在第一象限或第二象限，确定圆心与半径，可得所求的圆的方程．
解答 解：由题意可得所求的圆心在第一象限或第二象限，
圆心在第一象限，圆心为（2，2），半径为2，
故要求的圆的方程为（x-2）2+（y-2）2=4．
圆心在第二象限，圆心为（-2，2），半径为2，
故要求的圆的方程为（x+2）2+（y-2）2=4．
故答案为：（x-2）2+（y-2）2=4或（x+2）2+（y-2）2=4．
点评 本题主要考查用待定系数法求圆的标准方程的方法，求出圆心坐标和半径的值，是解题的关键，属于中档题．
练习册系列答案
相关题目
3．已知函数f（x）=2sin（ωx+φ）+1（0＜ω＜3，0＜φ＜$\frac{π}{2}$）的一系列对应值如下表：
（1）根据表格提供的数据求函败y=f（x）的解析式；
（2）求函数y=f（x）的单调递增区间与对称中心坐标；
（3）函数y=mf（x）-1在（-$\frac{π}{12}$，$\frac{π}{3}$）上有零点，求实数m的取值范围．
| x | -$\frac{π}{3}$ | -$\frac{π}{12}$ | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f（x） | -1 | 1 | 2 | 3 | 1 | -1 | 1 |
（2）求函数y=f（x）的单调递增区间与对称中心坐标；
（3）函数y=mf（x）-1在（-$\frac{π}{12}$，$\frac{π}{3}$）上有零点，求实数m的取值范围．
1．抛物线y2=8x上到其焦点F距离为4的点有（ ）个．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
8．直线y=-2x+b一定通过（ ）
| A． | 第一、三象限 | B． | 第二、四象限 | C． | 第一、二、四象限 | D． | 第二、三、四象限 |
18．若曲线y2=2px（p＞0）上只有一个点到其焦点的距离为1，则p的值为（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
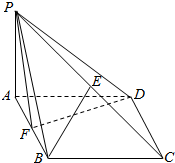如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BAD=45°，AB=2，AD=$\sqrt{2}$，PA⊥平面ABCD，E是PC的中点，F是AB的中点．