题目内容
1.设x,t满足约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-3≤0}\\{3x-2y+6≥0}\end{array}\right.$,向量$\overrightarrow{a}$=(y,a+x),$\overrightarrow{b}$=(2,-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,若令y=f(x),则f(x)=-2x-2a,a的最小值为-3.分析 由向量平行得出y关于x的函数y=-2x-2a,作出平面区域,当a最小时,直线y=2x-2a的截距最大,根据图象找到边界点,代入f(x)求出a.
解答  解:∵$\overrightarrow{a}$∥$\overrightarrow{b}$,∴-y-2(a+x)=0,∴y=-2x-2a.即f(x)=-2x-2a.
解:∵$\overrightarrow{a}$∥$\overrightarrow{b}$,∴-y-2(a+x)=0,∴y=-2x-2a.即f(x)=-2x-2a.
作出平面区域如图:
由图象可知当直线y=-2x-2a经过点C(3,0)时截距最大,即a最小.
把(3,0)代入y=-2x-2a得a=-3.
故答案为-2x-2a,-3.
点评 本题考查了平面向量的共线定理,线性规划,属于中档题.

练习册系列答案
相关题目
11.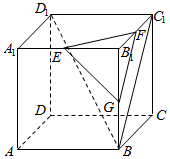 在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
 在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
12.已知定义在R上的函数y=f(x)满足f(2-x)=f(2+x),f(7-x)=f(7+x),f(3)=0,且该函数在区间[0,7]内再没有其它的值使f(x)=0,则此函数为( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
6.函数f(x)=2sin2($\frac{x}{2}$+$\frac{π}{4}$)-1是( )
| A. | 周期为π的奇函数 | B. | 周期为π的偶函数 | ||
| C. | 周期为2π的奇函数 | D. | 周期为2π的偶函数 |
9.若复数z=$\frac{a+3i}{i}$+a的实部为2,则复数z的虚部是( )
| A. | -i | B. | -3 | C. | 1 | D. | 2 |
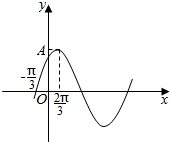 已知函数y=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图,则ω与φ的值分别为$\frac{1}{2}$,$\frac{π}{6}$.
已知函数y=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图,则ω与φ的值分别为$\frac{1}{2}$,$\frac{π}{6}$.