题目内容
抛物线C1:y=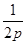 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
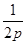 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )A.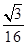 | B.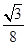 | C.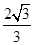 | D.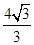 |
D
如图在同一坐标系中画出C1、C2草图,知C1焦点F(0, ),
),
C2右焦点F2(2,0).

由C2渐近线方程为y=± x.
x.
直线FF2方程为 +
+ =1.联立C1与直线FF2方程得
=1.联立C1与直线FF2方程得
①代入②得2x2+p2x-2p2=0.
设M(x0,y0),
即2 +p2x0-2p2=0.③
+p2x0-2p2=0.③
由C1得y′= x,
x,
所以 x0=
x0= ,即x0=
,即x0= p.④
p.④
由③④得p=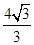 .故选D.
.故选D.
 ),
),C2右焦点F2(2,0).

由C2渐近线方程为y=±
 x.
x.直线FF2方程为
 +
+ =1.联立C1与直线FF2方程得
=1.联立C1与直线FF2方程得
①代入②得2x2+p2x-2p2=0.
设M(x0,y0),
即2
 +p2x0-2p2=0.③
+p2x0-2p2=0.③由C1得y′=
 x,
x,所以
 x0=
x0= ,即x0=
,即x0= p.④
p.④由③④得p=
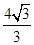 .故选D.
.故选D.
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
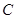 的右焦点为
的右焦点为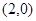 ,实轴长
,实轴长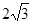 .
.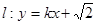 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点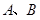 ,且
,且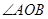 为锐角(其中
为锐角(其中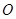 为原点),求
为原点),求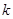 的取值范围.
的取值范围.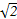 ,且过点P(4,-
,且过点P(4,-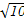 ).
).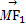 ·
· =0.
=0. 的离心率为
的离心率为 .若抛物线
.若抛物线 的焦点到双曲线
的焦点到双曲线 的渐近线的距离为
的渐近线的距离为 的方程为( )
的方程为( )



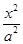 -y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
-y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )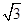 (B)
(B) 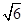 (C)2 (D)
(C)2 (D)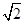 +1
+1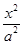 -
-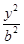 =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=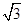 x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )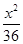 -
-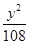 =1
=1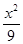 -
-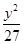 =1
=1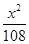 -
-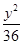 =1
=1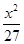 -
-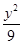 =1
=1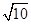 ,0),B(
,0),B(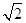 的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )
的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )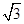
 ,实轴长为4,则双曲线的方程为 .
,实轴长为4,则双曲线的方程为 .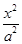 -
-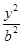 =1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为 .
=1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为 .