题目内容
已知抛物线y2=4x的焦点为F,准线为l,l与双曲线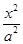 -y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
-y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
(A)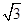 (B)
(B) 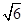 (C)2 (D)
(C)2 (D)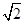 +1
+1
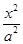 -y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
-y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )(A)
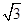 (B)
(B) 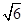 (C)2 (D)
(C)2 (D)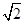 +1
+1B
抛物线y2=4x的焦点F(1,0),准线l:x=-1.
当x=-1时,由 -y2=1,
-y2=1,
得y2=-1+ .
.
∴A(-1, ),B(-1,-
),B(-1,- ),
),
∴ =(-2,
=(-2, ),
), =(-2,-
=(-2,- ).
).
∵△FAB为直角三角形,
∴ ·
· =0.
=0.
即4+1- =0,
=0,
∴a2= .
.
∴e= =
= =
= =
=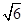 .
.
故选B.
当x=-1时,由
 -y2=1,
-y2=1,得y2=-1+
 .
.∴A(-1,
 ),B(-1,-
),B(-1,- ),
),∴
 =(-2,
=(-2, ),
), =(-2,-
=(-2,- ).
).∵△FAB为直角三角形,
∴
 ·
· =0.
=0.即4+1-
 =0,
=0,∴a2=
 .
.∴e=
 =
= =
= =
=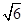 .
.故选B.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
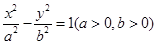 上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若
上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若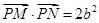 ,则该双曲线的离心率为____.
,则该双曲线的离心率为____.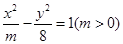 的一个焦点,则双曲线的离心率为( )
的一个焦点,则双曲线的离心率为( )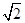
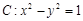 的左、右焦点,点P在C上,
的左、右焦点,点P在C上,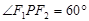 ,则P到x轴的距离为 ( )
,则P到x轴的距离为 ( )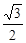
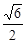
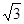
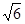
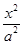 -
-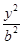 =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=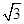 x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为 .
x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为 .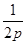 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )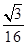
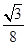
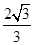
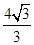
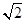
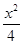 -
-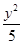 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|= |AF|,则A点的横坐标为( )
|AF|,则A点的横坐标为( )