题目内容
已知椭圆的中点在原点且过点 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.  或
或
试题分析:由题设可知,椭圆的方程是标准方程.
(1)当焦点在x轴上时,设椭圆方程为
 (a>b>0),则
(a>b>0),则 ,
,解得:
 ;所以 此时椭圆的方程是
;所以 此时椭圆的方程是 ;
;(2)当焦点在y轴上时,设椭圆方程为
 (a>b>0),则
(a>b>0),则 ,
,解得:
 ;所以此时所求的椭圆方程为
;所以此时所求的椭圆方程为 。
。综上知:椭圆的标准方程为
 或
或 。
。点评:本题主要考查了运算求解能力,分类讨论思想、方程思想.属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 -
- =1的离心率为e,抛物线x=2py2的焦点为(e,0),则p的值为( )
=1的离心率为e,抛物线x=2py2的焦点为(e,0),则p的值为( )

 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。 的长轴
的长轴 分成
分成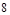 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于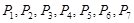 七个点,
七个点, 是椭圆的一个焦点,则
是椭圆的一个焦点,则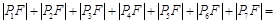 ( )
( )
 作直线
作直线 交双曲线
交双曲线 于
于 、
、 两点,且
两点,且 为
为 中点.
中点.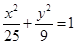 上一点
上一点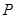 到一个焦点的距离为5,则
到一个焦点的距离为5,则 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且
为椭圆上一点,且 ,则
,则 的面积为
的面积为


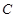 :
: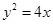 的焦点为
的焦点为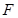 ,直线
,直线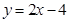 与
与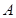 、
、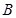 两点.则
两点.则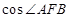 ="________."
="________."  与双曲线
与双曲线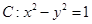 有且只有一个公共点,则
有且只有一个公共点,则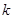 =
=