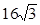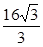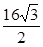题目内容
(本题满分12分)已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.
(Ⅰ)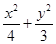 ="1." (Ⅱ)直线AE与x轴相交于定点Q(1,0)。
="1." (Ⅱ)直线AE与x轴相交于定点Q(1,0)。
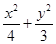 ="1." (Ⅱ)直线AE与x轴相交于定点Q(1,0)。
="1." (Ⅱ)直线AE与x轴相交于定点Q(1,0)。试题分析:(1)根据椭圆C:
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 得到a,c的比值,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
得到a,c的比值,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。那么利用线与圆相切,利用点到直线的距离公式得到圆的半径。求解得到结论。
=0相切。那么利用线与圆相切,利用点到直线的距离公式得到圆的半径。求解得到结论。(2)由题意知直线PB的斜率存在,设直线PB的方程为y=k(x-4).与椭圆方程联立,然后结合韦达定理,得到k的表达式,进而得到交点定点的坐标。
解:(Ⅰ)由题意知e=
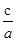 =
= ,所以e2=
,所以e2=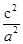 =
=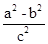 =
=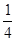 .即a2=
.即a2=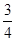 b2.
b2.又因为b=
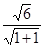 =
=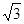 ,所以a2=4,b2=3.故椭圆的方程为
,所以a2=4,b2=3.故椭圆的方程为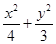 =1.…4分
=1.…4分(Ⅱ)由题意知直线PB的斜率存在,设直线PB的方程为y=k(x-4).
由
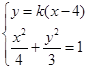 ,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分
,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分设点B(x1,y1),E(x2,y2),则A(x1,-y1).直线AE的方程为y-y2=
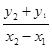 (x-x2).令y=0,得x=x2-
(x-x2).令y=0,得x=x2-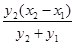 .将y1=k(x1-4),y2=k(x2-4)代入,
.将y1=k(x1-4),y2=k(x2-4)代入,整理,得x=
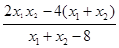 . ②…8分
. ②…8分由①得x1+x2=
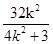 ,x1x2=
,x1x2=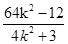 …10分 代入②整理,得x=1.
…10分 代入②整理,得x=1.所以直线AE与x轴相交于定点Q(1,0).……12分
点评:解决该试题的关键是熟练的运用椭圆的几何性质得到其椭圆的方程,以及联立方程组的思想,结合韦达定理得到k的值,求解得到定点。

练习册系列答案
相关题目
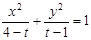 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: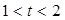 ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆. 上的一点,
上的一点, 、
、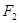 为该椭圆的两个焦点,若
为该椭圆的两个焦点,若 ,则
,则 的面积等于( )
的面积等于( )
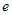 是椭圆
是椭圆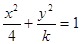 的离心率,且
的离心率,且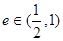 ,则实数
,则实数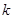 的取值范围是( )
的取值范围是( )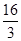 )
)  (
( 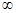 )
)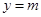 与椭圆
与椭圆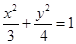 有两个不同的交点,则实数
有两个不同的交点,则实数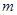 的取值范围是
的取值范围是 。
。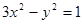 交于A,B两点.
交于A,B两点. 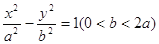 的左焦点
的左焦点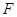 引圆
引圆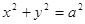 的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则
的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则 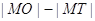 与
与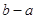 的大小关系为
的大小关系为 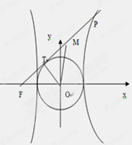
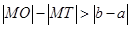
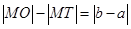
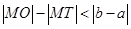
 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程. 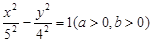 上一点,若
上一点,若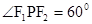 ,则三角形
,则三角形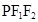 的面积为( )
的面积为( )