题目内容
20.若Sn是等差数列{an}的前n项和且S8-S3=20,则S11的值为( )| A. | 66 | B. | 48 | C. | 44 | D. | 12 |
分析 由等差数列{an}的前n项公式求出a1+5d=4,则此能求出S11的值.
解答 解:∵Sn是等差数列{an}的前n项和,且S8-S3=20,
∴(8a1+$\frac{8×7}{2}d$)-(3a1+$\frac{3×2}{2}d$)=20,
整理,得:5a1+25d=20,
∴a1+5d=4,
∴S11=$11{a}_{1}+\frac{11×10}{2}d$=11(a1+5d)=11×4=44.
故选:C.
点评 本题考查等比数列的前11项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
10. 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )| A. | 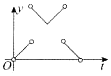 | B. | 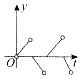 | C. | 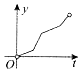 | D. | 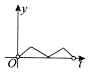 |
5.若有99%的把握说事件A与事件B有关,那么具体算出的X2一定满足( )
| A. | X2>10.828 | B. | X2<10.828 | C. | X2>6.635 | D. | X2<6.635 |
9.在△ABC中,∠A=60°,b=1,S△ABC=$\sqrt{3}$,则$\frac{a-2b+c}{sinA-2sinB+sinC}$的值等于( )
| A. | $\frac{{2\sqrt{39}}}{3}$ | B. | $\frac{26}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{3}$ | D. | $2\sqrt{3}$ |
10.已知对任意实数x,有f(-x)=-f(x),g(-x)=g(x),且x<0时,导函数分别满足f′(x)>0,g′(x)<0,则x>0时,成立的是( )
| A. | f′(x)>0,g′(x)<0 | B. | f′(x)>0,g′(x)>0 | C. | f′(x)<0,g′(x)<0 | D. | f′(x)<0,g′(x)>0 |