题目内容
16.设D为不等式组$\left\{\begin{array}{l}{x+\frac{y}{{t}^{2}}≤1}\\{({t}^{2}+1)x-y≥-{t}^{2}}\\{x-2y≤1}\end{array}\right.$,表示的平面区域,其中t为常数且0<t<1,点B(m,n)为坐标平面xOy内一点,若对于区域D内的任一点A(x,y),都有$\overrightarrow{OA}•\overrightarrow{OB}$≤1成立,则m+n的最大值等于1.分析 由约束条件作出可行域,求出三角形顶点的坐标,由$\overrightarrow{OA}•\overrightarrow{OB}$≤1得到关于m,n的不等式组,再作出可行域,由线性规划知识求得m+n的最大值.
解答 解:由约束条件$\left\{\begin{array}{l}{x+\frac{y}{{t}^{2}}≤1}\\{({t}^{2}+1)x-y≥-{t}^{2}}\\{x-2y≤1}\end{array}\right.$作出可行域如图,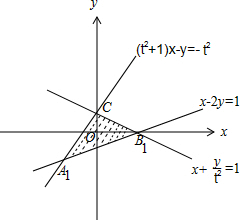
联立$\left\{\begin{array}{l}{({t}^{2}+1)x-y=-{t}^{2}}\\{x-2y=1}\end{array}\right.$,解得A1(-1,-1),
由$\overrightarrow{OA}•\overrightarrow{OB}$≤1,得mx+ny-1≤0,
∴$\left\{\begin{array}{l}{m-1≤0}\\{{t}^{2}n-1≤0}\\{m+n-1≤0}\end{array}\right.$,作出可行域如图,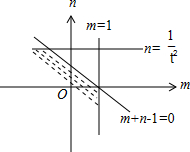
令z=m+n,由图可知,m+n的最大值等于1.
故答案为:1.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法及数学转化思想方法,考查计算能力,难度较大.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.已知定义在R上的函数f(x)关于直线x=1对称,若x≥1时,f(x)=x(1-x),则f(0)=( )
| A. | 0 | B. | -2 | C. | -6 | D. | -12 |
8.已知集合M={x|-4<x<3},N={x|lg(x+2)≤1},则M∩N=( )
| A. | (-2,3) | B. | (-2,8] | C. | (-4,3) | D. | (-4,8] |
6.函数f(x)=log3(x+1)+log3(5-x),则f(x)的( )
| A. | 最大值为3 | B. | 最大值为9 | C. | 最大值为2 | D. | 最小值为2 |