题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}满足b3=3,b5=9.
(1)分别求数列{an},{bn}的通项公式;
(2)设cn=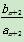 (n∈N*),求证:cn+1<cn≤
(n∈N*),求证:cn+1<cn≤ .
.
解 (1)由an+1=2Sn+1,①
得an=2Sn-1+1(n≥2,n∈N*),②
①-②得an+1-an=2(Sn-Sn-1),
∴an+1=3an(n≥2,n∈N*),
又a2=2S1+1=3,∴a2=3a1,∴an=3n-1.
∵b5-b3=2d=6,∴d=3,∴bn=3n-6.
(2)证明:∵an+2=3n+1,bn+2=3n,
 ∴cn+1<cn<…<c1=
∴cn+1<cn<…<c1= ,即cn+1<cn≤
,即cn+1<cn≤ .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
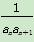 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn. =a10,2(an+an+2)=5an+1,则数列{an}的通项公式an=________.
=a10,2(an+an+2)=5an+1,则数列{an}的通项公式an=________.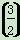 n-1
n-1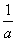 是函数f(x)的一个零点;
是函数f(x)的一个零点;