题目内容
10.奇函数f(x)满足件f(x+2)+f(x)=0,(x∈R),若x∈[0,1]时,f(x)=2x-1,则f(log${\;}_{\frac{1}{8}}$125)=-$\frac{1}{4}$.分析 根据函数奇偶性和条件判断函数的周期性,利用函数奇偶性和周期性的性质将条件进行转化求解即可.
解答 解:∵f(x)是奇函数,
∴f(-x)=-f(x),f(0)=0,
又∵f(x+2)+f(x)=0,
∴f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
即函数f(x)是周期为4的周期函数,
log${\;}_{\frac{1}{8}}$125=$\frac{lo{g}_{2}{5}^{3}}{lo{g}_{2}\frac{1}{8}}$=$\frac{3lo{g}_{2}5}{-3}$=-log25,
则f(log${\;}_{\frac{1}{8}}$125)=f(-log25)=-f(log25),
∵2<log25<3,
∴0<log25-2<1,
即0<log2$\frac{5}{4}$<1,
则f(log2$\frac{5}{4}$)=${2}^{lo{g}_{2}\frac{5}{4}}$-1=$\frac{5}{4}$-1=$\frac{1}{4}$,
即f(log${\;}_{\frac{1}{8}}$125)=f(-log25)=-f(log25)=-$\frac{1}{4}$,
故答案为:-$\frac{1}{4}$.
点评 本题考查函数值的计算,考查函数的奇偶性和周期性的应用以及利用周期性求函数值,体现转化的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知不等式loga(1-$\frac{1}{x+2}$)>0的解集是(-∞,-2),则a的取值范围是( )
| A. | 0<a$<\frac{1}{2}$ | B. | $\frac{1}{2}$<a<1 | C. | a>2 | D. | a>1 |
19.已知空间向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{CD}$,$\overrightarrow{AD}$,则下列结论正确的是( )
| A. | $\overrightarrow{AB}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{DC}$+$\overrightarrow{BC}$=$\overrightarrow{AD}$ | C. | $\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{DC}$ | D. | $\overrightarrow{BC}$=$\overrightarrow{BD}$-$\overrightarrow{DC}$ |
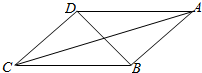 如图,在平行四边形ABCD中,已知AB=CD=a,AD=2a,∠DAB=60°,AC∩BD=E,将其沿对角线BD折成直二面角.
如图,在平行四边形ABCD中,已知AB=CD=a,AD=2a,∠DAB=60°,AC∩BD=E,将其沿对角线BD折成直二面角.