题目内容
11.已知关于x的一元二次方程9x2+6ax-b2+4=0,a,b∈R(1)若a是从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求已知方程有两个不相等实根的概率;
(2)若a是从区间[0,3]内任取一个数,b是从区间[0,2]内任取一个数,求已知方程有实根的概率.
分析 (1)列举出所有基本事件个数,及满足条件方程有两个不相等实根(△>0)的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)计算a是从区间[0,3]内任取一个数,b是从区间[0,2]内任取一个数,对应的基本事件的面积,及满足条件方程有实根的基本事件的面积,代入几何概型概率计算公式,可得答案.
解答 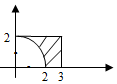 解:设事件A为“方程9x2+6ax-b2+4=0有2个不相等的实数根”,事件B为“方程9x2+6ax-b2+4=0有实数根”
解:设事件A为“方程9x2+6ax-b2+4=0有2个不相等的实数根”,事件B为“方程9x2+6ax-b2+4=0有实数根”
(1)由题意,知基本事件有9个,即(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)其中第一个表示a的取值,第二个数表示b的取值.
由△=36a2+36(-b2+4)=36a2+36b2-36×4>0得a2+b2>4
事件A要求a,b满足条件a2+b2>4,可知包含6个基本文件:(1,2),(2,2),(2,2),(3,0),(3,1),(3,2),
∴方程有2个不同实根的概率$P(A)=\frac{6}{9}=\frac{2}{3}$
(2)由题意方程有实根的区域为图中阴影部分,
∴所求概率为$P(B)=\frac{6-π}{6}=1-\frac{π}{6}$.
点评 本题考查的知识点是几何概型,古典概型,其中分析出满足条件的基本事件的实质是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知tanα=-$\frac{3}{4}$,且α是第二象限角,则cosα的值为( )
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
3.偶函数f(x)在(0,+∞)上递增,a=f(log2$\frac{1}{3}$)b=f($\frac{3}{2}$)c=f(log32),则下列关系式中正确的是( )
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
20.如图,某组合体的三视图是由边长为2的正方形和直径为2的圆组成,则它的体积为( )


| A. | 4+4π | B. | 8+4π | C. | $4+\frac{4}{3}π$ | D. | $8+\frac{4}{3}π$ |
1.设计一个计算1×3×5×7×9的算法,下面给出了算法语句的一部分,则在横线①上应填入下面数据中的( )

| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
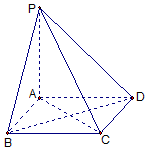 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.