题目内容
(本题满分14分)设 .
.
(1)判断函数 在
在 的单调性;
的单调性;
(2)设 为
为 在区间
在区间 上的最大值,写出
上的最大值,写出 的表达式.
的表达式.
 .
.(1)判断函数
 在
在 的单调性;
的单调性;(2)设
 为
为 在区间
在区间 上的最大值,写出
上的最大值,写出 的表达式.
的表达式.(1)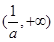 为函数
为函数 的单调增区间,
的单调增区间,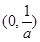 为函数
为函数 的单调减区间;
的单调减区间;
(2)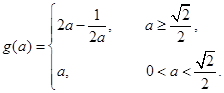
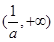 为函数
为函数 的单调增区间,
的单调增区间,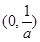 为函数
为函数 的单调减区间;
的单调减区间;(2)
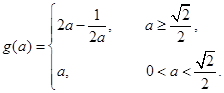
(1)先求出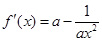 ,然后根据导数大(小)于零,研究其单调性即可.
,然后根据导数大(小)于零,研究其单调性即可.
(II)在(I)的基础上,要根据a的取值范围讨论它在[1,2]上的单调性,进而可确定出f(x)在[1,2]上的最大值.注意连续函数在闭区间上的最值问题不在极值处取得就在区间端点处取得.
解:(1)由已知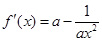 ,
,
注意到 ,
,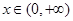 ,
,
解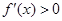 ,得
,得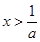 ;解
;解 ,得
,得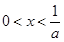 .
.
所以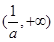 为函数
为函数 的单调增区间,
的单调增区间,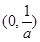 为函数
为函数 的单调减区间. ……5分
的单调减区间. ……5分
(2)由(1)知
当 ,即
,即 时,
时, 的最大值为
的最大值为 ; …………2分
; …………2分
当 ,即
,即 时,
时, 的最大值为
的最大值为 ; …………2分
; …………2分
当 ,即
,即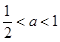 时,
时,
因为 ,
,
所以,当 时,
时, 的最大值为
的最大值为 , …………2分
, …………2分
当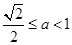 时,
时, 的最大值为
的最大值为 , …………2分
, …………2分
综上, …………1分
…………1分
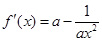 ,然后根据导数大(小)于零,研究其单调性即可.
,然后根据导数大(小)于零,研究其单调性即可.(II)在(I)的基础上,要根据a的取值范围讨论它在[1,2]上的单调性,进而可确定出f(x)在[1,2]上的最大值.注意连续函数在闭区间上的最值问题不在极值处取得就在区间端点处取得.
解:(1)由已知
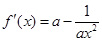 ,
,注意到
 ,
,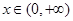 ,
,解
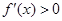 ,得
,得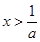 ;解
;解 ,得
,得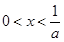 .
. 所以
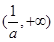 为函数
为函数 的单调增区间,
的单调增区间,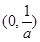 为函数
为函数 的单调减区间. ……5分
的单调减区间. ……5分(2)由(1)知
当
 ,即
,即 时,
时, 的最大值为
的最大值为 ; …………2分
; …………2分当
 ,即
,即 时,
时, 的最大值为
的最大值为 ; …………2分
; …………2分当
 ,即
,即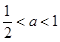 时,
时, 因为
 ,
,所以,当
 时,
时, 的最大值为
的最大值为 , …………2分
, …………2分当
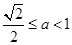 时,
时, 的最大值为
的最大值为 , …………2分
, …………2分综上,
 …………1分
…………1分
练习册系列答案
相关题目
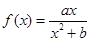 在
在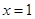 处取得极值为2,设函数
处取得极值为2,设函数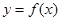 图象上任意一点
图象上任意一点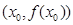 处的切线斜率为k。
处的切线斜率为k。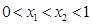 ,存在k,使得
,存在k,使得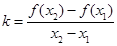 ,求证:
,求证: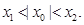

 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围; 且关于x的方程
且关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 满足:
满足: 求证:
求证:
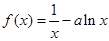 .(
.(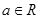 )
)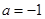 时,试确定函数
时,试确定函数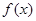 在其定义域内的单调性;
在其定义域内的单调性;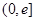 上的最小值;
上的最小值;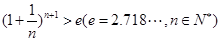 .
. 的对称中心为
的对称中心为 ,记函数
,记函数 的导函数为
的导函数为 ,
, ,则有
,则有 .若函数
.若函数 ,则可求得
,则可求得






 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为_____ .
,则切点的横坐标为_____ . 的导数是( )
的导数是( )



 ,则
,则 等于
等于



 ,若
,若 ,则
,则 的值
的值