题目内容
 如图为一个几何体的三视图,尺寸如图所示(不考虑接触点),
如图为一个几何体的三视图,尺寸如图所示(不考虑接触点),(1)画出这个几何体的直观图;
(2)求这个几何体的体积(结果保留根号、π).
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图可以看出,此几何体由一个半径为1的球体与一底面边长为2的直三棱柱所组成,故可求这个几何体的体积.
解答:
 解:(1)由三视图知,此组合体上部是一个半径为
解:(1)由三视图知,此组合体上部是一个半径为
的球体,下部为一直三棱柱,其高为3,底面为一边长为2的正三角形,且题中已给出此三角形的高为
,直观图如图所示;
(2)几何体的体积V=
×2×
×3+
π×(
)3=3
+
.
 解:(1)由三视图知,此组合体上部是一个半径为
解:(1)由三视图知,此组合体上部是一个半径为| 1 |
| 2 |
| 3 |
(2)几何体的体积V=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查对三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是表面积.三视图的投影规则是主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等.

练习册系列答案
相关题目
设集合S={A0,A1,A2,A3},在S上定义运算⊕:Ai⊕Aj=Ak,其中k为i+j被4除的余数(其中i,j=0,1,2,3),则满足关系式(x⊕x)⊕A2=A0的x(x∈S)的个数为( )
| A、4 | B、3 | C、2 | D、1 |
设椭圆的两个焦点分别为F1、F2,过F2作椭圆长轴的垂线交椭圆于点M,若△F1F2M为等腰直角三角形,则椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
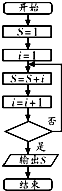 阅读如图的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于16,那么在程序框图中的判断框内应填写的条件是( )
阅读如图的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于16,那么在程序框图中的判断框内应填写的条件是( )| A、i>5? | B、i>6? |
| C、i>7? | D、i>8? |