题目内容
某化工厂生产某种产品，每件产品的生产成本是3元，根据市场调查，预计每件产品的出厂价为x元(7≤x≤10)时，一年的产量为(11－x)2万件，若该企业所生产的产品全部售出，则称该企业正常生产，但为了保护环境，用于治理污染的费用与产量成正比，比例系数为常数a(1≤a≤3)．
(1)求该企业正常生产一年的利润L(x)与出厂价x的函数关系式；
(2)当每件产品的出厂价定为多少元时，企业一年的利润最大，并求最大利润．
(1)依题意，L(x)＝(x－3)(11－x)2－a(11－x)2＝(x－3－a)(11－x)2，x∈[7,10]．
(2)因为L′(x)＝(11－x)2－2(x－3－a)·(11－x)＝(11－x)(11－x－2x＋6＋2a)＝(11－x)(17＋2a－3x)．
由L′(x)＝0，得x＝11∉[7,10]或x＝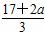
.
因为1≤a≤3，
所以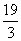
≤≤
.
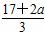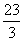①当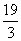≤≤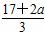7，即1≤a≤2时，L′(x)在[7,10]上恒为负，则L(x)在[7,10]上为减函数，所以L(x)max＝L(7)＝16(4－a)．
②当7<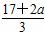≤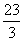，即2<a≤3时，
L(x)max＝L()＝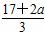
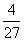(8－a)3.
当1≤a≤2时，在每件产品出厂价为7元时，年利润最大，为16(4－a)万元．当2<a≤3时，在每件产品出厂价为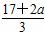元时，年利润最大，为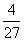(8－a)3万元．
练习册系列答案
相关题目
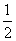，3]，则函数F(x)＝f(x)＋
的值域是( )
]
，
＋1)＝lgx，求f(x)的解析式．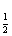
x|的定义域是[a，b]，值域为[0,2]，对于区间[m，n]，称n－m为区间[m，n]的长度，则[a，b]长度的最小值为( )
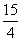B．3
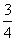
的值域是( )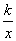
＋
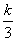在(1，＋∞)上是增函数，则实数k的取值范围是( )