题目内容
已知函数f（x）=（1-a）x2-ax-1
（1）若函数只有一个零点，求实数a的取值范围；
（2）如果函数的一个零点为2，求a的值．
（1）若函数只有一个零点，求实数a的取值范围；
（2）如果函数的一个零点为2，求a的值．
考点：函数零点的判定定理,二次函数的性质
专题：计算题,函数的性质及应用
分析：（1）由题意可化为方程f（x）=（1-a）x2-ax-1=0有一个根，从而讨论求解；
（2）由题意得f（2）=4（1-a）-2a-1=0，从而解得．
（2）由题意得f（2）=4（1-a）-2a-1=0，从而解得．
解答：
解：（1）当1-a=0，即a=1时，f（x）=-x-1，
函数有且只有一个零点-1；
当1-a≠0，即a≠1时，
△=a2+4（1-a）=0，
解得，a=2；
故a=1或a=2；
（2）由题意得，
f（2）=4（1-a）-2a-1=0，
解得，a=
．
函数有且只有一个零点-1；
当1-a≠0，即a≠1时，
△=a2+4（1-a）=0，
解得，a=2；
故a=1或a=2；
（2）由题意得，
f（2）=4（1-a）-2a-1=0，
解得，a=
| 1 |
| 2 |
点评：本题考查了二次函数的应用及函数零点的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知α∈（π，2π），cosα=-
，tan2α=（ ）
| ||
| 5 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
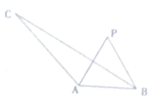如图所示，在△ABC中，∠BAC=120°，AC=3，AB=1，P为∠BAC平分线上异于A的一点，∠APB=α，三角形PAB的面积记为S．（1）求BC的长；
（2）若α∈[
| π |
| 6 |
| π |
| 3 |
定义一种新运算：a?b=
，已知函数f（x）=（1+
）?log
x，若函数g（x）=f（x）-k恰有两个零点，则k的取值范围为（ ）
|
| 2 |
| x |
| 2 |
| A、（1，2] |
| B、（1，2） |
| C、（0，2） |
| D、（0，1） |