题目内容
已知数列{an}的各项均为正数,其前n项和为Sn,且2Sn=an2+an,n∈N.
(1)求数列{an}的通项公式;
(2)设bn=
,求证:对一切正整数n,有b1+b2+…+bn<
.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| an2 |
| 7 |
| 4 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)由2Sn=an2+an,知2Sn-1=an-12+an-1,(n≥2),作差得(an-an-1-1)(an+an-1)=0,由此说明数列为等差数列,由等差数列的通项公式得答案;
(2)把(1)中求得的通项公式代入bn=
,放大后裂项,利用裂项相消法求和后可得结论.
(2)把(1)中求得的通项公式代入bn=
| 1 |
| an2 |
解答:
(1)解:由2Sn=an2+an,①
得2Sn-1=an-12+an-1(n≥2),②
①-②即得(an-an-1-1)(an+an-1)=0,
∵an>0,∴an-an-1=1,
又2S1=2a1=a12+a1,得a1=1,
∴an=n(n∈N*);
(2)证明:bn=
=
<
=
-
(n≥2),
当n=1时,b1=1<
,
当n=2时,b1+b2=1+
=
<
,
当n≥3时,b1+b2+…+bn<1+
+
-
+
-
+…+
-
=
-
<
.
∴对一切正整数n,有b1+b2+…+bn<
.
得2Sn-1=an-12+an-1(n≥2),②
①-②即得(an-an-1-1)(an+an-1)=0,
∵an>0,∴an-an-1=1,
又2S1=2a1=a12+a1,得a1=1,
∴an=n(n∈N*);
(2)证明:bn=
| 1 |
| an2 |
| 1 |
| n2 |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
当n=1时,b1=1<
| 7 |
| 4 |
当n=2时,b1+b2=1+
| 1 |
| 4 |
| 5 |
| 4 |
| 7 |
| 4 |
当n≥3时,b1+b2+…+bn<1+
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 7 |
| 4 |
| 1 |
| n |
| 7 |
| 4 |
∴对一切正整数n,有b1+b2+…+bn<
| 7 |
| 4 |
点评:本题是数列与不等式的综合题,考查了等差关系的确定,训练了裂项相消法求数列的和,考查了放缩法证明数列不等式,是中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
正方体ABCD-A1B1C1D1中,AB1与C1D1所成的角( )
| A、30° | B、45° |
| C、60° | D、90° |
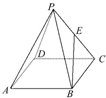 如图所示,正四棱锥P-ABCD的底面积为3,体积为
如图所示,正四棱锥P-ABCD的底面积为3,体积为