题目内容
8.已知△ABC的三边a,b,c所对的角分别为A,B,C,且sinA:sinB:sinC=2:3:$\sqrt{7}$.(1)求角C;
(2)若△ABC的面积为6$\sqrt{3}$,求$\frac{c}{sinC}$的值.
分析 (1)由已知及正弦定理可得:a:b:c=2:3:$\sqrt{7}$,设a=2x,则b=3x,c=$\sqrt{7}$x,由余弦定理可求得cosC=$\frac{1}{2}$,结合范围C∈(0,π),可得C的值.
(2)由三角形面积公式可求得:ab=24,又由(1)得:a:b:c=2:3:$\sqrt{7}$,即可解得a,b,c的值,从而可求$\frac{c}{sinC}$的值.
解答 解:(1)∵sinA:sinB:sinC=2:3:$\sqrt{7}$,
∴由正弦定理可得:a:b:c=2:3:$\sqrt{7}$,
∴设a=2x,则b=3x,c=$\sqrt{7}$x,由余弦定理可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{4{x}^{2}+9{x}^{2}-7{x}^{2}}{2×2x×3x}$=$\frac{1}{2}$,
∴由C∈(0,π),可得:C=$\frac{π}{3}$.
(2)∵C=$\frac{π}{3}$.
∴△ABC的面积为6$\sqrt{3}$=$\frac{1}{2}$absinC=$\frac{1}{2}$×ab×$\frac{\sqrt{3}}{2}$,解得:ab=24.
又∵由(1)可得:a:b:c=2:3:$\sqrt{7}$,
∴解得:a=4,b=6,c=2$\sqrt{7}$,
∴$\frac{c}{sinC}$=$\frac{2\sqrt{7}}{sin\frac{π}{3}}$=$\frac{4\sqrt{21}}{3}$.
点评 本题主要考查了正弦定理,三角形面积公式,比例的性质,余弦定理在解三角形中的应用,考查了转化思想和计算能力,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
18.设集合M={x||x|≤5,x∈N},P={x|x>1},则M∩P=( )
| A. | {2,3,4} | B. | {2,3,4,5} | C. | {1,2,3,4,5} | D. | {x|1<x≤5,x∈R} |
3.若数列{an}的通项公式an=$\frac{1}{2+4+6+…+2n}$,且前n项和为Sn,则S2015=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{4028}{2015}$ | D. | $\frac{2014}{4030}$ |
13.从一个边长为2的等边三角形的中心、各边中点及三个顶点这7个点中任取两个点,则这两点间的距离小于1的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
1.已知三棱锥O-ABC的顶点A,B,C都在半径为2的球面上,O是球心,∠AOB=60°,当△AOC和△BOC的面积之和最大时,则O到面ABC的距离为( )
| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{2\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{7}$ | D. | $\frac{{2\sqrt{21}}}{7}$ |
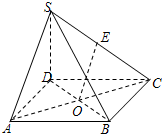 如图四棱锥S-ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6.
如图四棱锥S-ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6.