题目内容
10.已知函数f(x)=sinx+2cos2$\frac{x}{2}$-1,g(x)=$\sqrt{2}$sin2x,则下列结论正确的是( )| A. | 把函数f(x)图象上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移$\frac{π}{4}$个单位长度,可得到函数g(x)的图象 | |
| B. | 两个函数的图象均关于直线x-=-$\frac{π}{4}$对称 | |
| C. | 两个函数在区间(-$\frac{π}{4}$,$\frac{π}{4}$)上都是单调递增函数 | |
| D. | 函数y=g(x)在[0,2π]上只有4个零点 |
分析 利用二倍角的余弦公式、两角和的正弦公式化简函数的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性、零点,以及图象的对称性,得出结论.
解答 解:函数f(x)=sinx+2cos2$\frac{x}{2}$-1=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),g(x)=$\sqrt{2}$sin2x,
故把函数f(x)图象上各点的横坐标缩短到原来的一半(纵坐标不变),可得y=$\sqrt{2}$sin(2x+$\frac{π}{4}$)的图象,
再向右平移$\frac{π}{4}$个单位长度,可得到函数y=$\sqrt{2}$sin(2x-$\frac{π}{4}$),故A不正确;
当x=-$\frac{π}{4}$时,f(x)=$\sqrt{2}$sin0=0,不是函数的最值,故B错误;
在区间(-$\frac{π}{4}$,$\frac{π}{4}$)上,x+$\frac{π}{4}$∈(0,$\frac{π}{2}$),2x∈(-$\frac{π}{2}$,$\frac{π}{2}$),f(x)和g(x)在区间(-$\frac{π}{4}$,$\frac{π}{4}$)上都是单调递增函数,故C正确;
在[0,2π]上,令g(x)=$\sqrt{2}$sin2x=0,求得x=0,$\frac{π}{2}$,π,$\frac{3π}{2}$π,2π,故函数y=g(x)在[0,2π]上共计有5个零点,故D错误,
故选:C.
点评 本题主要考查二倍角的余弦公式、两角和的正弦公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性、零点,以及图象的对称性,属于基础题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.国际上通常用恩格尔系数衡量一个国家和地区人民生活水平的状况,它的计算公式为$n=\frac{x}{y}$(x代表人均食品支出总额,y代表人均个人消费支出总额)且y=2x+475,各种类型的家庭标准如表:
张先生居住区2007年比2002年食品支出下降7.5%,张先生家在2007年购买食品和2002年完全相同的情况下人均少支出75元.则张先生家2007年属于( )
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n≤59% | 40%≤n≤50% | 30%≤n≤40% |
| A. | 贫困 | B. | 温饱 | C. | 小康 | D. | 富裕 |
1.不等式$\frac{x-1}{{x}^{2}-4}$>0的解集为( )
| A. | {x|-2<x<1} | B. | {x|-2<x<1或x>2} | C. | {x|x>2} | D. | {x|1<x<2或x<-2} |
5.函数f(x)=2x+x-2的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
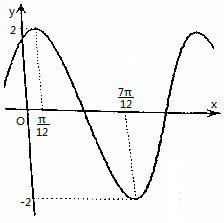 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图. 在如图所示的四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥CD,BC⊥平面PAB,且E、M、N分别为PD、CD、AD的中点,$\overrightarrow{PF}=3\overrightarrow{FD}$.
在如图所示的四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥CD,BC⊥平面PAB,且E、M、N分别为PD、CD、AD的中点,$\overrightarrow{PF}=3\overrightarrow{FD}$.